Мотоциклист выехал из города со скоростью v = 60 км/ч, и одновременно ему
навстречу из деревни выехал велосипедист со скоростью u. Через время t = 30 мин они встретились. Затем мотоциклист доехал до деревни, сразу же с удвоенной скоростью поехал назад
и успел в город одновременно с велосипедистом. Найдите скорость велосипедиста u и расстояние S между городом и деревней.
2 лайка
Эту задачу можно решать как аналитически, так и графически. Сначала аналитический способ.
Расстояние мотоциклиста от города по пути в деревню равно x=vt (пусть \tau является временем прибытия мотоциклиста в деревню, тогда это уравнение справедливо для интервала времени 0<t<\tau). По пути обратно его координата описывается уравнением x=L-v(t-\tau)=2L-vt (поскольку расстояние между городом и деревней равно L=v\tau).
Координата велосипедиста (как и раньше, относительно города) описывается функцией y=L-ut. В какой-то момент времени t=t_1=30\space мин мотоциклист встречает велосипедиста, то есть x(t_1)=y(t_1). Встречаются они и сразу у города, то есть в конце их координаты x(t_2)=y(t_2)=0. Эти два уравнения записываются в виде:
vt_1 =L-ut_1, \qquad
\begin{cases}
2L-vt_2=L-ut_2 \\
L-ut_2 = 0
\end{cases}
Из второй системы уравнений сразу получаем, что v=2u (оно и было сразу очевидно из того, что за один отрезок времени мотоциклист и велосипедист проехали расстояния 2L и L). Из первого уравнения получается
L = (v+u)t_1 = 3vt_1/2=45\spaceкм.
Этот ответ тоже можно было получить очень быстро: относительно мотоциклиста велосипедист движется со скоростью v+u, а значит L=(v+u)t_1.
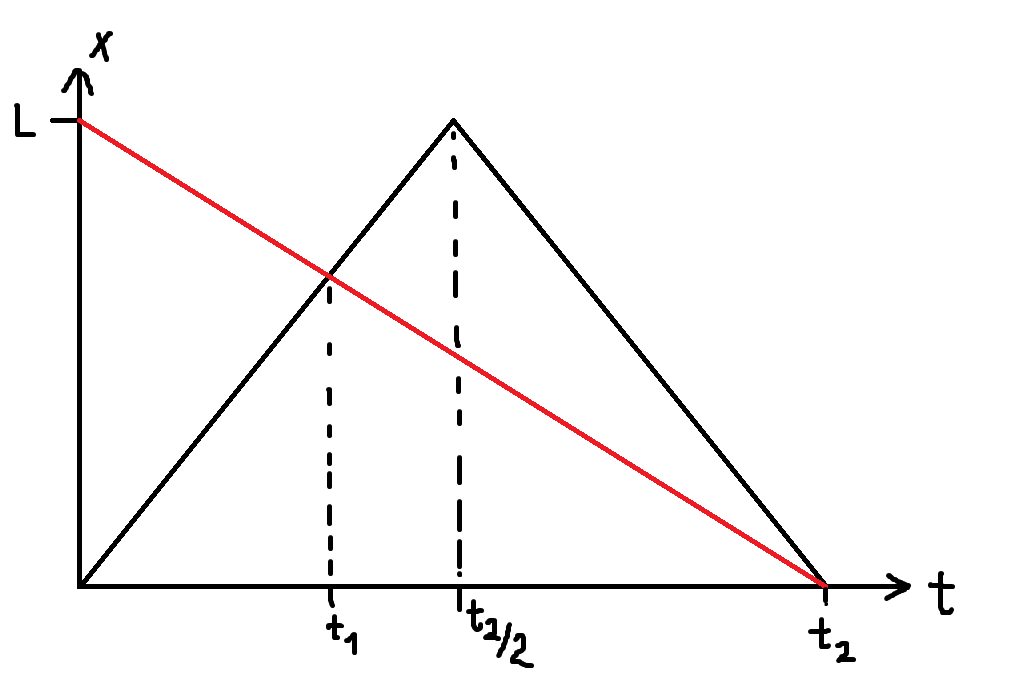
Графический способ в этой задаче, сразу скажу, бесполезный, он тупо сводится к составлению аналитических уравнений (просто может быть кому-нибудь визуально понятнее тогда будет). График получается таким (чёрная ломаная описывает движение мотоциклиста, красная – велосипедиста):
Тем не менее, иногда в кинематике появляются такие задачи, в которых сильно запаришься расписывать уравнения с кучей неизвестных параметров, зато они решаются довольно легко графически.
8 лайков