Так. Для начала напишу задание в виде текста, потому что вдруг кто-то будет в поисковике искать решение.
Задачник “1001 задача по физике”, Гельфгат.
1.19**.
По прямому шоссе со скоростью v_1 = 16 м/с движется автобус. На расстоянии d = 60 м от шоссе и s = 400 м от автобуса находится человек. Человек может бежать со скоростью v_2 = 4 м/с. В каком направлении он должен бежать, чтобы успеть «перехватить» автобус, который к нему приближается? При какой наименьшей скорости человека v_2min это вообще возможно? В каком направлении следует при этом бежать?
Решение:
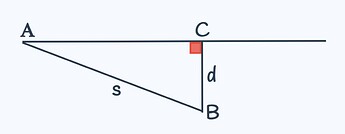
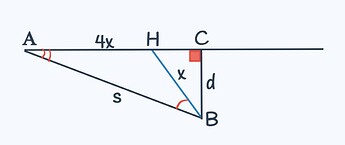
Для начала нарисуем шоссе в виде луча с началом в точке А — это начальное положение автобуса.
На некотором расстоянии снизу от шоссе отметим точку В — это начальное положение человека.
BC — расстояние(перпендикуляр) от человека до шоссе, равное d.
AB — расстояние от человека до автобуса, равное s.
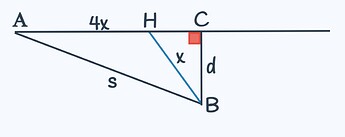
Сначала рассмотрим вариант с наименьшим углом для бега. В этом случае человек и автобус прибудут в точку H_1 одновременно, т.е. t_1 = t_2
Так как скорость автобуса в 4 раза больше скорости человека, а время у них одинаковое, то автобус проедет в 4 раза больше. Отметим путь человека как x. Тогда путь автобуса — 4x.
Начинается самое интересное.
Найдём угол \angle CAB.
sin \angle CAB = \dfrac{d}{s} = \dfrac{60}{400} = 0,15
Значит \angle CAB = 9^{\circ}
Теперь используем теорему синусов и находим наш угол \angle ABH_1.
\dfrac{x}{sin \angle CAB} = \dfrac{4x}{sin \angle ABH_1}
\dfrac{x}{0,15} = \dfrac{4x}{sin \angle ABH_1}
sin \angle ABH_1 = 0,6
\angle ABH_1 = 37^{\circ} (т.к. наш угол острый)
Значит, минимальный угол, под которым человек может бежать к автобусу — 37^{\circ}.
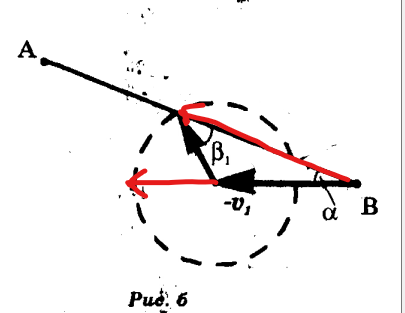
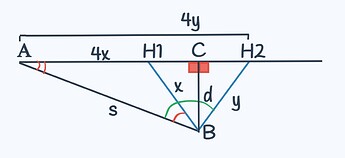
Теперь по той же логике найдём максимальный угол.
В этом случае человек и автобус прибудут в точку H_2 снова одновременно и их время снова будет равно, а значит автобус снова проедет в 4 раза больше, чем человек. Пусть путь человека — y. Тогда путь автобуса — 4y.
Нам нужно найти угол
\angle ABH_2.
Снова воспользуемся теоремой синусов:
\dfrac{y}{sin \angle CAB} = \dfrac{4y}{sin \angle ABH_2}
\dfrac{y}{0,15} = \dfrac{4y}{sin \angle ABH_2}
sin \angle ABH_2 = 0,6
\angle ABH_2 = 143^{\circ} (т.к. наш угол тупой)
Вот и всё.
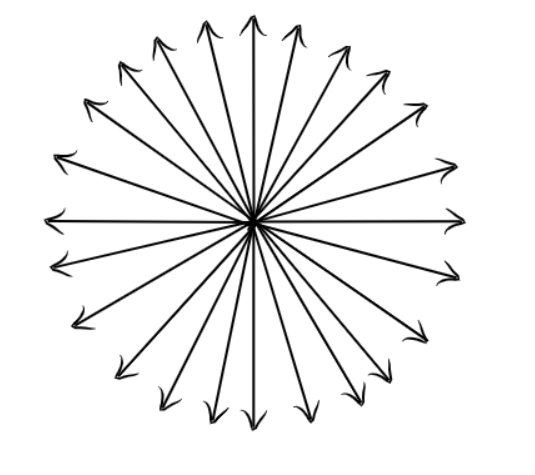
Для того, чтобы “перехватить” автобус, угол бега человека должен быть в промежутке
37^{\circ} \leq \alpha \leq 143^{\circ}.
А вот чтобы найти минимальную скорость v_2min, нужно скорость человека умножить на \dfrac {d}{s}, т.е. 4 \times 0,6 = 2,4 м/с.