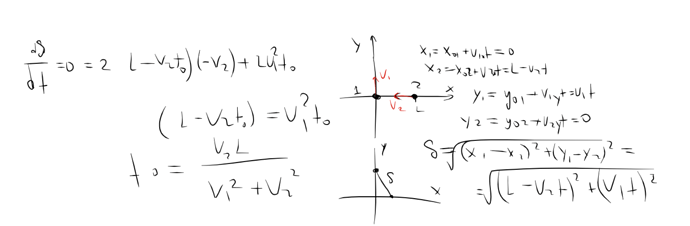Условие: Два автомобиля движутся с постоянными скоростями v1 и v2 по дорогам, пересекающимся под прямым углом. Когда первый автомобиль достиг перекрестка, второму оставалось проехать до этого места расстояние L. Спустя какое время t после этого расстояние между автомобилями будет наименьшим? Чему равно это расстояние Smin?
Ответ посмотрел, решение не понял, можете объяснить?
Чтобы понять такую задачу, удобно провести аналогию с более простыми задачами. Для этого рассмотрим ход решения задачи:
Два автомобиля движутся с постоянными скоростями v_1 и v_2 по дороге, навстречу друг к другу. Через какое время они встретятся, если изначальное расстояние между ними l?
Её можно решать двумя способами.
- Втупую. Пишем уравнение движения для каждого автомобиля и решаем эту систему
- Через размышления. Машины движутся друг навстречу другу с постоянными скоростями, значит скорость их сближения тоже постоянна и равна v_1 + v_2. И тогда можем записать t = \frac {l} {v_1 + v_2}.
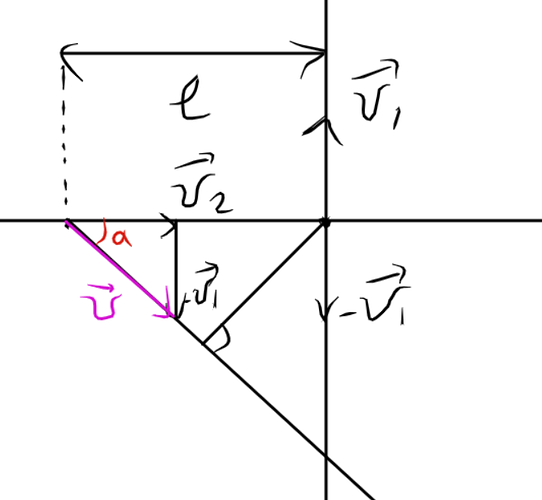
Но ко второму способу можно прийти и другим методом. Мы рассматриваем не скорость сближения, а движение первой машины, относительно второй. Для этого отнимем от каждой скорости скорость второй машины. Графически это будет выглядеть так:
Тогда скорость второй машины будет равняться нулю, а скорость первой v_1 + v_2 в сторону второй. Дальнейший ход решения тривиален.
Вернёмся к начальной задаче. Если есть решение, добавь его, пожалуйста, в вопрос, а потом попытайся понять его проводя аналогию с упрощенной задачей. Если же решения нет, полезным будет ещё немного посидеть над задачей, перед тем как читать решение
Если и теперь не получилось
Её тоже можно рассматривать двумя способами:
- Расписать уравнение движения для каждого автомобиля, найти зависимость расстояния от времени и взять производную (что является энергозатратным и очень сильно увеличивает риск ошибки в виде забытого минуса или двойки, но является полезным для решения во время подготовки, если уже знаешь производные)
- Рассмотреть движение второго автомобиля относительно первого. Для этого проделаем те же манипуляции, что и в подготовительной задаче. Отнимем от каждого автомобиля скорость первого. Графически это выглядит так:
Дальнейшее решение сводиться к геометрии и t = \frac s v}
Спасибо огромное:)
Если ты знаешь производные то можешь сделать так как я показал, то есть когда функция S(t)=Smin, dS/dt=0. Но ее можно решить одним шагом перейдя в систему отчета одного из машин. Попробуй сам сделать
Лучше попробую геометрией, производными и дифференциалами не знаком)