Савченко 5.2.8*

Физика Термодинамика
1

5.2.8∗
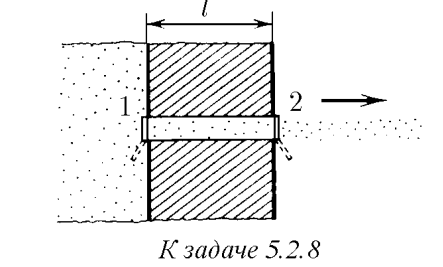
. В толстой стенке сосуда, содержащего газ, сделан прямой канал длины l, который соединяет сосуд с вакуумным пространством. Для формирования
пучка молекул канал снабжен двумя затворами. Затвор 1 расположен на выходе
канала в сосуд, затвор 2 — на выходе канала в вакуумное пространство. Пучок
молекул формируется следующим образом: сначала на время τ открывают затвор 1, затем, после того как этот затвор закроется, через время t0 открывается
на время τ затвор 2. Молекулы, пролетевшие во время этого процесса канал, образуют в вакуумном пространстве пучок. Чему равна длина этого пучка через
время t после закрывания затвора 2?

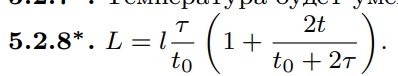
image
image1040×243 63.8 KB

image
Ответ:
image
У меня много вопросов к этой задаче, большинство формата: “За что?” и “Почему?”.
А если серьёзно задача из темы про распределение молекул газа по скоростям, и как вообще расстояние связано с временем в частности t_0 и \tau(хотя тут ещё более менее ясно) я понять не в состоянии, прошу подсказать хотя бы с чего начать, пожалуйста

2

Попробуй ответить на вопрос “какая скорость молекулы должна быть, чтобы она успела залететь с одной стороны и вылететь с другой?” У тебя возникнут некоторые неравенства.

3

ну я получил вот это \frac{l}{t_0} > v > \frac{l}{t_0+2\tau}, если скорость больше верхнего предела то частица рикошетит от затвора, а если меньше то она не успеет долететь до второго затвора. дальше
L = v_{max}(t+\tau) - v_{min}t. t + \tau потому что она вылетела под начало открытия 2, а отсчёт t идёт с закрытия.
L = \frac{l}{t_0}(t+\tau)-\frac{l}{t_0+2 \tau}t даём общий знаменатель
L = \frac{l}{t_0(t_0 + 2 \tau)}(tt_0+t_0\tau +2t\tau+ 2\tau^2-tt_0) после дальнейших преобразований получаем
L=l\frac{\tau}{t_0(t_0+2\tau)}(t_0+2t+2\tau)
L=l\frac{\tau}{t_0}(1+\frac{2t}{t_0+2\tau}), что совпадает с ответом в задачнике.

3 лайка