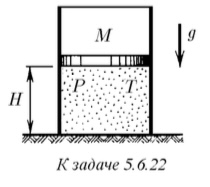
В откачанном пространстве вертикально стоит цилиндрический со- суд, перекрытый сверху подвижным поршнем массы M. Под поршнем находится одноатомный газ при температуре T и давлении P. Внутреннее сечение цилин- дра S, высота той части сосуда, внутри которой находится газ, H. Поршень от- пустили. Он начал двигаться. Чему равна максимальная скорость, развиваемая поршнем, если газ сжимается изотермически? адиабатически?
1 лайк
a) Из закона сохранения энергии или теоремы о кинетической энергии и работе
\frac{Mv^2}{2} = Mg(H-y) + A \;(1)
где A - работа, совершенная над поршнем, равная работе, совершенной газом, которая в данном случае (изотермический процесс) определяется как
A = nRT\ln{\frac{Sy}{SH}} = -nRT\ln{\frac{H}{y}} \;(2)
Подставляя (2) в (1)
\frac{Mv^2}{2} = Mg(H-y) - nRT\ln{\frac{H}{y}} \;(3)
Из закона Бойля-Мариотта
PSH = P'Sy \;(4)
Применение уравнения состояния к начальному состоянию,
n = \frac{PSH}{RT} \;(5)
PSH = nRT
Применение второго закона Ньютона
Mg - P(t)S = M\frac{dv}{dt}
В момент максимальной скорости dv/dt = 0 и P(t) = P', следовательно
Mg = P'S \;(6)
Подставляя (6) в (4) и выражая y
y = \frac{PSH}{Mg} \;(7)
Подставляя (5) и (7) в (3) и выделяя v
\boxed{v = \sqrt{2gH\left(1-\frac{PS}{Mg}+\frac{PS}{Mg}\ln{\frac{PS}{Mg}}\right)}}
b) Из закона Пуассона
P(SH)^\gamma = P'(Sy)^\gamma \;(8)
Работа, совершаемая газом при адиабатическом процессе, равна
A = \frac{PSH-P'Sy}{\gamma-1} \;(9)
Согласно (6), мы можем модифицировать (8) и выразить y, получив
y = H\left(\frac{PS}{Mg}\right)^\frac{1}{\gamma} \;(10)
Подставляем (9) в (1) и учитываем (6),
\frac{Mv^2}{2} = H\left(Mg+\frac{PS}{\gamma-1}\right)-Mgy\left(1+\frac{1}{\gamma-1}\right) \;(11)
Подставляя (10) в (11), поскольку газ одноатомный (i = 3 и \gamma = 5/3), и отделяя v
\boxed{v = \sqrt{2gH\left[1-\frac{5}{2}\left(\frac{PS}{Mg}\right)^\frac{3}{5}+\frac{3}{2}\frac{PS}{Mg}\right]}}
Источник: savchenko-physics.github.io
5 лайков