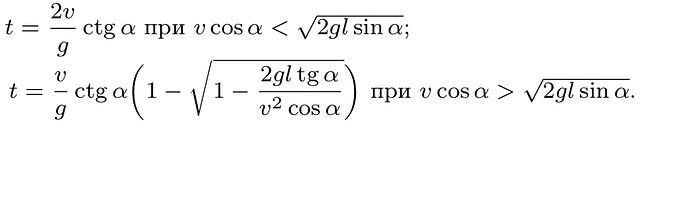Савченко 1.3.16*

Физика Механика
1

В трубу длины l, наклоненную под углом а к горизонту, влетает
шарик с горизонтальной скоростью v. Определите время пребывания шарика в трубе, если удары шарика о ее стенки упругие.
Здравствуйте,вот мои попытки решения:

IMG_5925
IMG_59251512×2016 732 KB

Использовал закон сохранения энергии,но ответ не выходит:
IMG_5924
IMG_59241170×338 36.5 KB

В чем моя ошибка?Обьясните пожалуйста

3

У меня:v<=2*sqrt(gsinal)
Ответ:v<=sqrt(2glsina)
Время я нашел,а скорость для двух разных случаев не совпадает с ответом

4

Почему ты взял работу силы тяжести дважды?

1 лайк
5

А ой,спасибо!

6

А почему время для второго случая стоит только с минусом?Почему знак «+» убрали из дискриминанта?

7

второй корень это случай когда он выйдет полетает чуточку и вернётся обратно, то есть второй раз окажется в точке с такой же координатой, но спрашивают когда он выйдет, то есть первый раз пройдёт через эту точку

3 лайка
8

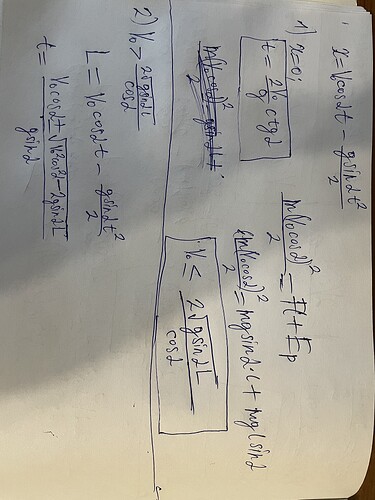
a) Найдем условие, при котором соудареня будут отсутсвовать (x=0)
Из закона сохранения энергии:

\frac{mv_0^2}{2} = mgl \cdot \sin \alpha
v_{0}\leq\frac{\sqrt{2gl\sin \alpha}}{\cos\alpha}

В этом случае пройдет время

t = \frac{2v_0}{g} \text{ctg} \alpha

b) Теперь рассмотрим те случаи, когда происходит касание:

v_{0}>\frac{\sqrt{2gl\sin \alpha}}{\cos\alpha}

Путь между двумя касаниями:

L=v_{0}\cos\alpha t-\frac{g\sin\alpha t^{2}}{2}

При получении необходимого времени выбираем именно тот, который меньший, т.к. необходимо найти время когда он выйдет

t=\frac{v_{0}\cos\alpha-\sqrt{v_{0}^{2}\cos^{2}\alpha-2g\sin\alpha L}}{g\sin\alpha}

Источник: savchenko-physics.github.io

4 лайка