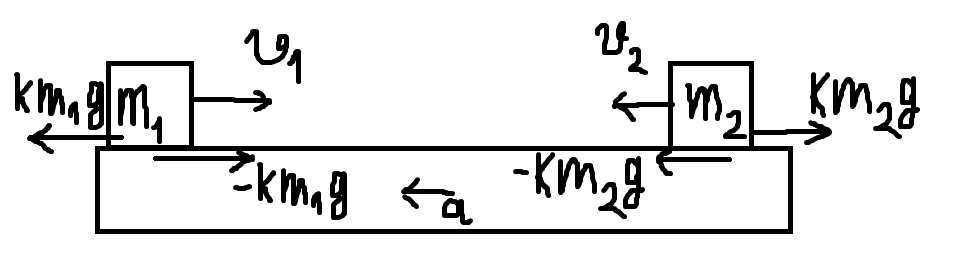
С противоположных концов однородного изначально неподвижного бруска длиной
L, лежащего на гладкой горизонтальной поверхности, навстречу друг другу пустили две
маленькие шайбы. Массы шайб m_1 = m и m_2 = 2m, их начальные скорости v_1 = v_0 и v_2 = 2v_0,
коэффициенты трения скольжения между бруском и шайбами одинаковы. Шайбы столкнулись
на середине бруска через время τ = 0,4L/v_0, имея при этом ненулевые скорости относительно
бруска. Найдите массу бруска M и коэффициент трения скольжения k шайб по бруску.
Ускорение свободного падения равно g. Будет ли задача иметь решение, если τ = 0,2L/v_0? τ = L/v_0? Ответ обоснуйте.
2 лайка
Так как нам нужно проанализировать задачу для разных значений τ, не будем пока что делать никаких предположений относительно значения τ и решим задачу в общем виде.
Запишем уравнения движения в этой системе. Так как есть силы трения на шайбы, направленные противоположно их скоростям, эти же силы трения согласно третьему закону Ньютона действуют в противоположном направлении на брусок (то есть в конечном итоге они сонаправлены скорости). Прежде чем перейти к этим уравнениям, скажу, что ускорения шайб a_1 и a_2 направлены против их скоростей, и имея это в виду, минусы расставлять не буду, держа в уме эти направления. Запись второго закона Ньютона:
m_1a_1 = km_1g \newline
m_2 a_2= km_2g\newline
Ma = km_2g - km_1g
Далее в условии сказано, что шайбы столкнулись ровно в середине бруска. В системе отсчёта, связанной с бруском, ускорение шайбы m_1 равно a_1-a, а второй шайбы - a_2+a. Значит,
L/2 = v_1τ-\frac{(a_1-a)τ^2}{2}=v_2τ-\frac{(a_2+a)τ^2}{2}
Так же важно то, что при определённых значениях данных параметров скорости v_1+V и v_2-V относительно бруска (чья скорость в момент времени 0<t<τ равна V=at и направлена вдоль v_2) могут обнулиться. То есть важным условием является то, что в момент соударения скорости имеют ненулевое значение:
v_1-a_1τ≥-aτ \newline
v_2 -a_2τ ≥ aτ
3 лайка