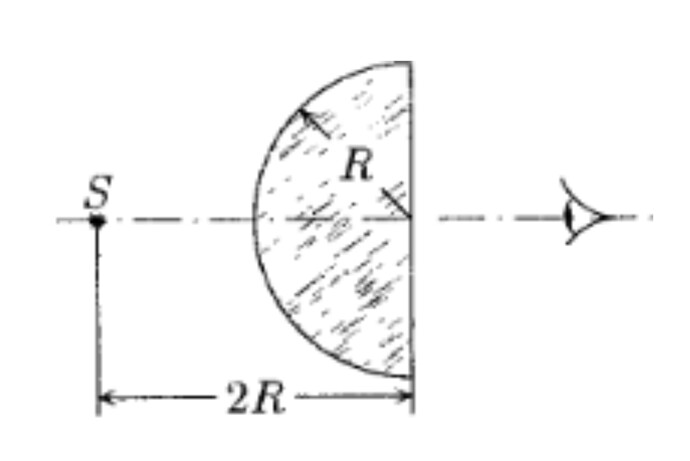
Из стеклянной пластинки с показа- телем преломления n = 1,5 вырезали толстую линзу в форме полушара радиусом R = 10 см. Через такую линзу рассматри- вается точечный источник света S, расположенный на рассто- янии a = 2R от плоской поверхности полушара (см. рисунок). На каком расстоянии от этой поверхности наблюдатель видит источник света?
Указание. Для малых углов tg α ≈ sin α ≈ α
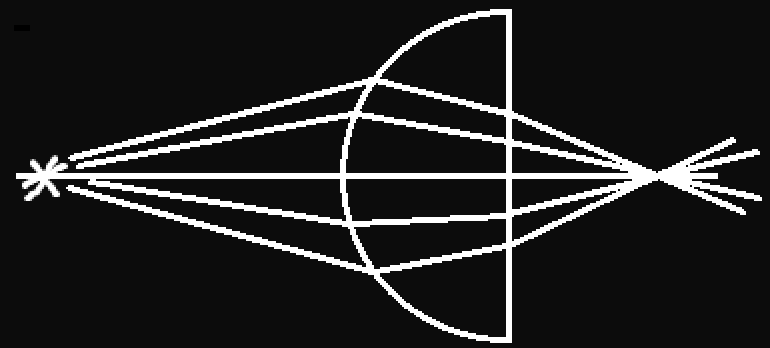
нарисуй оптический ход выходящих лучей и нарисуй их мнимые продолжения на выходе из линзы: это и будет мнимое изображение, которое видит наблюдатель.
Почему изображение мнимое ?
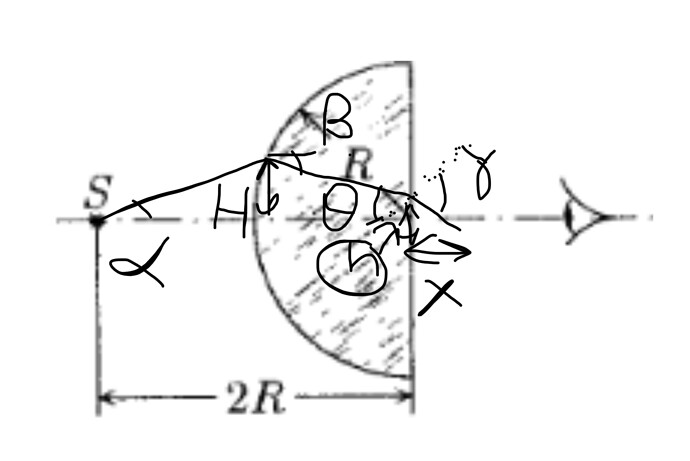
Обычно задачи такого типа решаются же как-то так (рис.)
Ответ если выйти в минус то значит мнимое но я не могу найти решение, у меня выходит 5 формул но 6 не как не могу найти
Ну в общем-то это несущественно: если по рисунку, так уж и быть, получится, что лучи сходятся в какой-то точке, то изображение действительное; если они расходятся, но их продолжения сходятся, то изображение мнимое. Это всё зависит от расположения действительного источника.
Ну тут получается, что изображение действительно. Надеюсь, теперь ты понимаешь что к чему.
тогда покажи как ты пытаешься найти x из твоей картинки)
у тебя нормаль к точке на сферической поверхности изображена неправильно – ею является радиус окружности
Ок, спасибо. Но тогда как решить задачу с правильной нормали?
Ого спасибо сейчас попробую
Вот решение
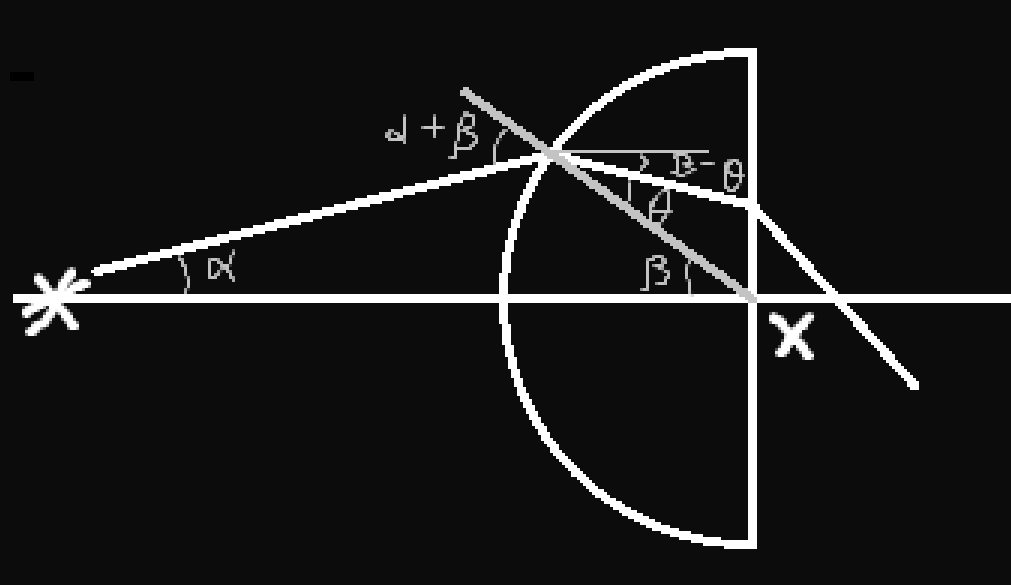
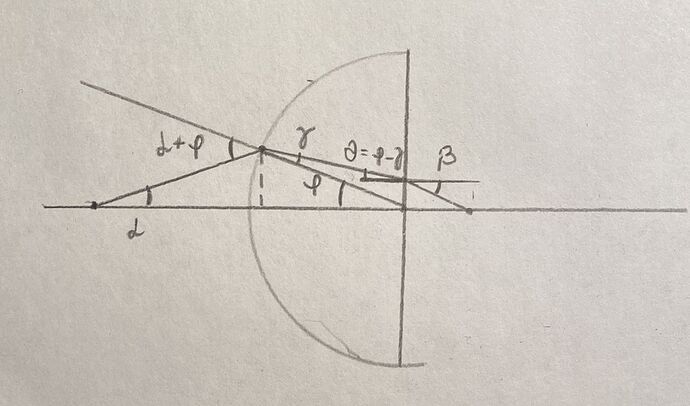
для углов на картинке можно записать \gamma=(\alpha+\phi)/n и \beta=n(\phi-\gamma). Вместе с этим \alpha=R\phi/(a-R)=\phi. Отсюда можно выразить все углы через угол \phi.
Тогда высота, на которой луч пересекает плоскую поверхность будет h=R\gamma=2R\phi/n, откуда x=h/\beta = \frac{2R\phi}{n} /(\phi n(1-\frac{2}{n})=\frac{2R}{n(n-2)}
Получится отрицательный ответ, что значит изображение будет мнимым.