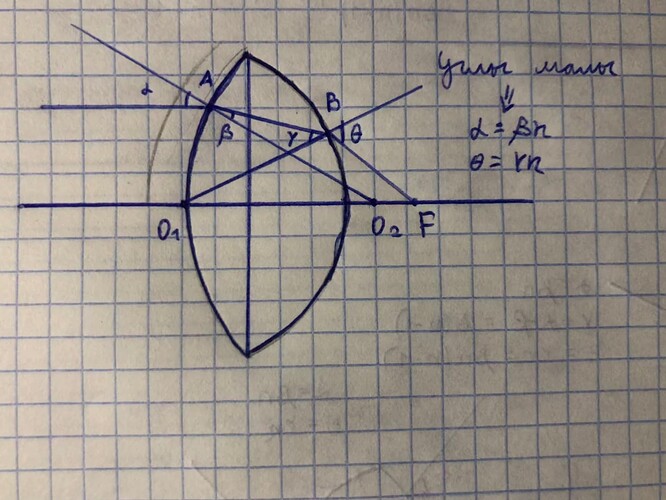
Найти оптическую силу линзы с радиусами сферических поверхностей R1 и R2. Показатель преломления материала - n.
Начал с построения, нарисовал ход луча, применил закон Снеллиуса с учетом малости углов. Что дальше - непонятно
Для вывода таких формул гораздо проще использовать принцип таутохронизма. Если расположить на главной оптической оси линзы точечный источник, то все параксиальные лучи, вышедшие из этого источника, соберутся в другой точке, то есть в изображении. Что это значит? Принцип таутохронизма постулирует то, что эти лучи прошли одинаковый оптический путь. Если луч прошёл в среде с показателем преломления n какой-то путь l, то его оптический путь равен \Delta=nl. Для неоднородной среды \Delta=\int ndl
Если линза тонкая, то практически все лучи, преломившись через неё, попадут в изображение. Так что тебе достаточно рассмотреть два луча: луч, прошедший через главную оптическую ось и луч, прошедший через самый край линзы.
Здесь и далее поверхность A имеет кривизну R_1, поверхность B – R_2. Источник P находится на расстоянии a от линзы, а его изображение – на расстоянии b.
Равенство оптических путей:
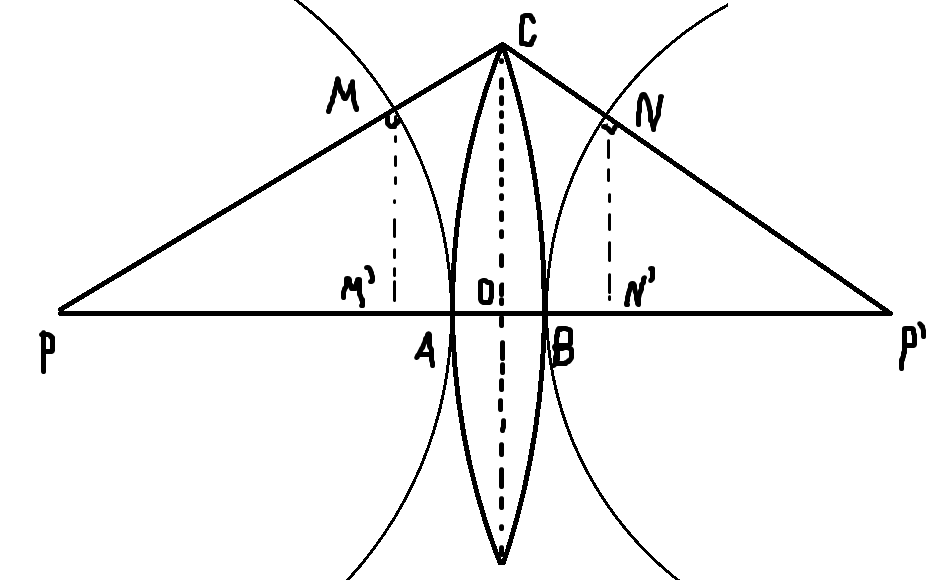
Существует такой способ решения: начерчу-ка я две окружности с центрами P и P' и радиусами PA=a и P'B=b
Так как все лучи расходятся изотропно по всем направлением, то ясно, что оптические длины лучей в пределах этих сфер одинаковы. Когда же луч преломляется через линзу, то нужно, чтобы прошедшая им оптическая длина nAB была равна оптической длине MCN другого луча. Так как лучи должны быть параксиальными, то допустимо считать, что M'ON'≈MCN.
Теперь нужно выразить эти величины через радиусы R_1 и R_2. Пусть OC=R, тогда AO равен радиусу кривизны R_1 минус \sqrt{R_1^2-R^2} (на рисунке центры окружности R_1 и R_2 не указаны). Применяя приближённую формулу (1+x)^n≈1+nx для малых x, получаем:
Аналогично выполняю и для M'A, OB и BN'. Следует иметь в виду то, что AO и BN' надо брать со знаком плюс, а M'A и OB с минусом, так как направления кривизн различные (это дело произвольного выбора направления).
Сокращая на R, наконец-то получаю формулу тонкой линзы:
Перед 1/a у меня получился минус из-за правила знаков. Попробуй теперь вывести формулу сферического зеркала. Ещё связанная с этим тема: Принцип Ферма — Википедия.