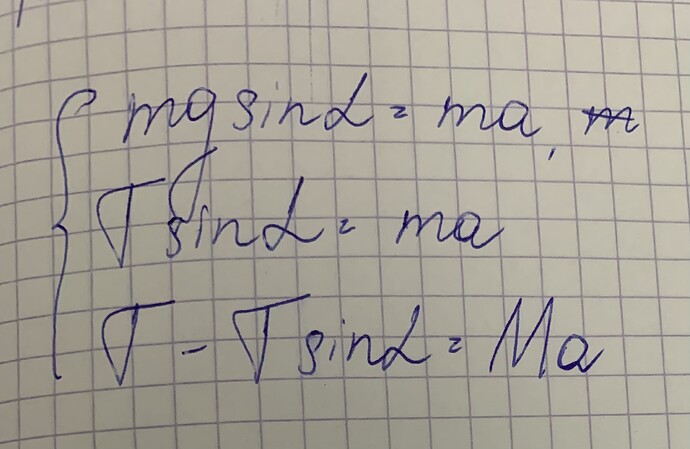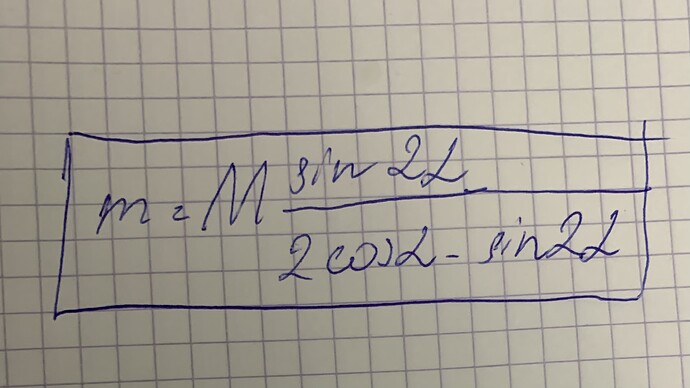Задача О-32. В механической системе, изображенной на рисунке, брусок массой М может скользить по рельсам без трения. В начальный момент подвешенный на нити груз отводят на угол \alpha от вертикали и отпускают. Какова масса m этого груза, если угол, образуемый нитью с вертикалью, не меняется при движении системы?
Ответ: m = \frac{\sin 2 \alpha }{2 \cos \alpha - \sin 2 \alpha}
Что-то не выходит ответ как в книге
Моя попытка решения задачи, можете подсказать где у меня ошибка, просто никак не выходит sin2α и 2cosα-sin2α
1 лайк
Вам в первую очередь нужно применить уравнение связей и решить их в системе , а именно:
Решая в совокупности , можно получить ответ
2 лайка
Первое уравнение неверное, там должно быть ma=mg \cos{\alpha}-T
я написал также, но что-то не вышло, на 2 картине
точно , не заметил
Зачем так усложнять? Выразите T, подставьте все и найдите ускорение. Это обычная система с 3 уравнениями и 3 неизвестными, избавьтесь от ненужных величин
5 лайков
Можете помочь пожалуйста, что-то опять не выходит, долго думал, попробовал еще один способ но там корень кубический выходит
@Max_Planck, Самое интересное, что эту задачу можно решить всего двумя уравнениями.
T \sin\alpha = ma
T - T \sin\alpha = Ma
Поделив одно уравнение на другое, получим:
m = M \sin\alpha / (1 - \sin\alpha)
Самое интересное, что это правильный ответ, так как
\sin\alpha / (1 - \sin\alpha) = \sin2\alpha / (2\cos\alpha - \sin2\alpha)
Не знаю почему автор решил так замудрить
4 лайка
Можете подробнее, почему вы убрали из системы уравнений проекцию груза массы m относительно оси ОУ. А также как вы получили из уравнения
\sin\alpha / (1 - \sin\alpha) = \sin2\alpha / (2\cos\alpha - \sin2\alpha)
ma = mg \cos\alpha - T
Это уравнение абсолютно верное. Я просто заметил что двух уравнении записанных выше сообщением достаточно для того чтоб решить задачу
А про тригонометрию, почему те уравнение равны, нужно просто знать формулу синуса двойного угла:
\sin2\alpha = 2 * \sin\alpha * \cos\alpha
Можешь подставить эту формулку в авторский ответ и увидишь что мой ответ не отличается от авторского
3 лайка
Там разве синус? Где ma=
Очепятался((
Теперь исправил 
3 лайка
Спасибо большое, а мы так можем сделать? То есть параметр просто убрать из системы
Мы же ничего не нарушаем. Мы также можем его использовать и все равно придем к конечному ответу. Я просто заметил что если поделить то уравнение на то другое уравнение, то сила натяжение T и ускорение a сократятся \to и выходит ответ
1 лайк
Спасибо, понял 
2 лайка