Тело, движущееся с постоянной скоростью v попадает в область, в которой на него
начинает действовать постоянная сила F. Спустя время τ скорость тела становится 2v,
направленной перпендикулярно начальной. С какой скоростью и под каким углом к
начальному курсу из этой области вылетело бы тело, имевшее начальную скорость 3v?
Просят найти значение скорости после вылета из области. Значит, первое, что нужно понять: какая толщина у области. В условии ни прямо, ни косвенно она не задана, значит мы можем предполагать, что область достаточно большая, чтобы тело успело повернуться.
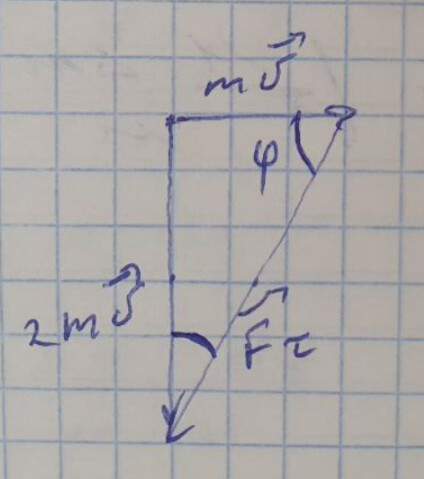
Далее, нужно найти силу и угол, под которым она действует. Это очень просто делается через векторную диаграмму. Векторная диаграмма – способ представления сложения векторов. Чтобы её нарисовать, сначала нужно расписать уравнение движения в векторном виде. Используем второй закон Ньютона в импульсном виде:
Уравнение и векторная диаграмма для первого случая
Где u – скорость через время t. Далее подставляем значения из условия и рисуем векторную диаграмму:
Уравнение для второго случая, но его теперь надо расписать по осям
Остаётся лишь решить эти уравнения
Решение уравнений для второго случая
По аналогии, с движением под углом к горизонту, мы можем рассматривать движение по двум осям по отдельности, а потом просто найти полную скорость по теореме Пифагора.