Савченко 1.4.9 относительность

Физика
1

Тело налетает на стенку со скоростью v пол углом α к линии, перпен-
дикулярной стенке. Определите скорость тела после упругого удара, если стенка:
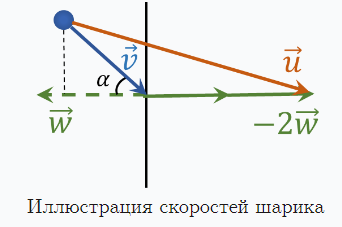
а) неподвижна; б) движется перпендикулярно самой себе со скоростью w навстре-
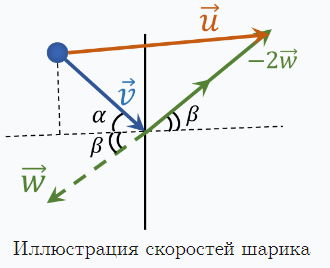
чу телу; в) движется под углом β к линии, перпендикулярной ей самой, со ско-
ростью w навстречу телу.
Можете помочь с примером б,я решал через ЗСС нашел скорасть относительно стенки и понял что надо к этой скорасти в СО земли прибавить скорасть стенки, но вопрос у меня повявился про геометрическую составляющюю
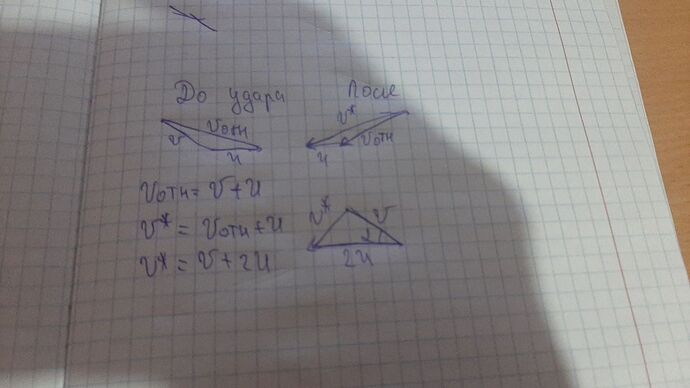
Если Vотн=v-w
u(конечная скорасть)=vотн+w
Тогда u=v?
Ну если сказать что vотн=v+w(что мы добавляем этот вектор, ну я это видел у пенкина)
Тогда получаеться u=v+2w
Но тогда конечном итоге у меня не получилась получить ответ

IMG_20240406_172415_817
IMG_20240406_172415_8171280×720 76 KB

Vотн^2 как я понял v^2+w^2+2vwcosa

2

а) Т.к. соударение упругое, то по Закону Сохранения Импульса:

v \sin \alpha = u \sin \alpha
\fbox{$v = u $}

б) Далее эта задача немного напоминает 1.4.8.
В системе отсчета связанной со стенкой относительная скорость шарика \vec{v_{отн}} = \vec{v} - \vec{w}. При упругом отражении, переходя в СО земли скорость равняется

\vec{u} = \vec{v} - 2\vec{w}

Ниже наглядно продемонстрирована работа с векторными величинами
image

Найдем проекции вектора \vec{u} на горизонтальную и вертикальные оси:

u_y = v \sin \alpha
u_x = v \cos \alpha + 2w

Воспользовывшись т. Пифагора, найдем модуль вектора \vec{u}

u = \sqrt{u_x^2+u_y^2}
u = \sqrt{(v \sin \alpha)^2 + (v \cos \alpha + 2w)^2}
\fbox{$u=\sqrt{v^{2}+4vw\cos\alpha+4w^{2}}$}

в) Аналогично предыдущему подпункту

\vec{u} = \vec{v} - 2\vec{w}

Покажем эти вектора на рисунке
image

Найдем проекции вектора \vec{u} на горизонтальную и вертикальные оси:

u_y = v \sin \alpha - 2w \sin \beta
u_x = v \cos \alpha + 2w \cos \beta

Воспользовывшись т. Пифагора, найдем модуль вектора \vec{u}

u = \sqrt{u_x^2+u_y^2}
u = \sqrt{(v \sin \alpha - 2w \sin \beta)^2 + (v \cos \alpha + 2w \cos \beta)^2}
\fbox{$u=\sqrt{v^{2}+4vw\cos\alpha\cos\beta+4w^{2}\cos^{2}\beta}$}

Источник: savchenko-physics.github.io

4 лайка