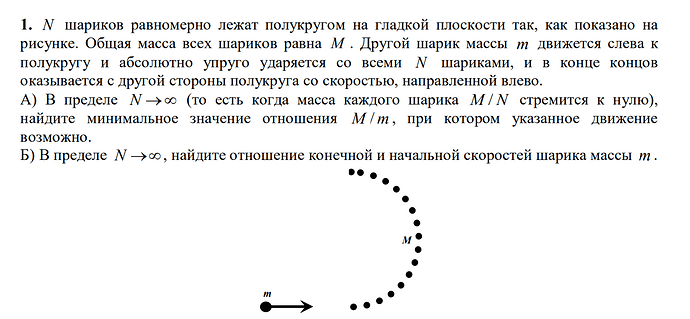
Тут возник вопрос имеет ли значение расположение шаров массой m? Каким образом следует выражение для переданной для всех шаров импульса?
2 лайка
Да, имеет. Это придаёт задаче симметричности, и задача разбивается на N одинаковых подзадач о том, что шарик массой m должен удариться о шарик массой M/N так, чтобы угол отклонения первого шарика был равным \pi/N.
Для того, чтобы приступить к решению этой задачи, нужно использовать результат следующего ответа на вопрос: на какой максимальный угол может отклониться шарик массой M, если он упруго ударился о покоящийся шарик массой m<M?
Для решения пункта Б нужно знать формулировку второго замечательного предела.
4 лайка
Да решал такое, там через производные находил, что cos(a)=sqrt(1-(m1/m2)^2), то есть sin(a)=m1/m2
и теперь просто подставить a=π/N, m1=M/N, m2=m?
1 лайк
Если учитывать то, что \alpha мал, то N сократятся и у тебя выйдет ответ первого пункта
1 лайк
А второй пункт решается просто уравнениями сохранения импульса и энергии, учитывая предел N?
Найди выражение для скорости шарика после удара с максимальным углом отклонения и упрости его через приближения первого порядка (когда пренебрегаешь величинами, высшими по порядку относительно \frac{M}{mN}). Таких ударов происходит всего N раз, поэтому все эти скорости образуют геометрическую прогрессию. И в самом конце применяешь то, о чём я сказал ранее:
5 лайков