Зависимость парциального давления насыщенного пара от кривизны поверхности фазовой границы

[Alisher (Alisher Yerkebayev)]

Как понятно из названия, меня интересует вопрос о том, каким образом давление пара зависит от кривизны поверхности. В известной мне научной литературе это объясняется вот так:

Рассмотрим обычный капилляр радиусом r, который погрузили над плоской поверхностью жидкости. Пусть поверхность абсолютно смачивающая, тогда радиус мениска равен радиусу капилляра, и добавочное давление определяется формулой Лапласа:

\Delta p = \frac{2\sigma}{r},

а так как вода поднимается на h, то и \Delta p = \rho g h, т.е.

h= \frac{2\sigma}{\rho gr}.

Давление насыщенных паров зависит только от температуры, но считая пар идеальным газом, нужно в таком случае учесть барометрическое (и изотермическое) изменение давления с высотой:

p=p_0 \exp \left (-\frac{\mu g h}{RT} \right).

Если подставить h, то получаем

p=p_0 \exp \left(-\frac{2\sigma \mu}{\rho r RT} \right).

В случае, если изменение этого давления относительно невелико, то, применяя \exp x ≈1+x при малых x, получаю

p=p_0 \left (1-\frac{2\sigma \mu}{\rho r RT} \right).

Если поверхность выпуклая, то нужно провести замену r → -r.
К тому же, эта формула в принципе распространяется на разные случаи, хотя вывод и был для капиллярной трубки над плоской поверхностью жидкости (например, давление пара над сферической поверхностью капли воды в тумане). Появляется вопрос: чем качественно объясняется такое явление и почему подобная экстраполяция допустима?

[Alisher (Alisher Yerkebayev)]

Нашёл!

Для всякого бесконечно малого процесса энтропия, вообще говоря, удовлетворяет неравенству:

dS \geq \frac{\delta Q}{T}.

Так как в дальнейшем все процессы будем считать изотермическими, то, используя свободную энергию Гельмгольца \Psi=U-TS, продифференцирую его при постоянной температуре, т.е. d\Psi_T=dU-TdS. Выражая первый закон термодинамики \delta Q = dU + \delta A, получу:

d\Psi_T≤-\delta A,

иначе говоря, внешняя работа -\delta A над системой, вообще говоря, больше изменения свободной энергии. Если система изолирована, то \delta A=0, а значит d\Psi_T\leq0, т.е. в термодинамически стабильном состоянии свободная энергия \Psi минимальна.

То же самое происходит и с термодинамическим потенциалом Гиббса \Phi=\Psi+PV. Так как d\Phi=d\Psi+PdV+VdP=d\Psi+\delta A+VdP, то при постоянной температуре и с учётом сказанного выше получаю

d\Phi\leq-VdP.

Теперь потихоньку будем подходить к самой задаче. Так как речь идёт о процессе на границе раздела жидкости с газом, то механическая устойчивость требует того, чтобы dP=0, то есть опять же получается, что \Phi стремится к минимуму.

Для равновесии двух фаз нужно, чтобы потенциалы Гиббса были равны. Рассмотрим систему из двух фаз с массами m_1 и m_2. Потенциал \Phi в сумме равен

\Phi=m_1\varphi_1+m_2\varphi_2,

где \varphi_1 и \varphi_2 являются удельными термодинамическими потенциалами. Массы могут превращаться в друг друга, но полная масса системы неизменна, а значит dm_1=-dm_2. Кроме того, происходящие процессы должны быть направлены в сторону уменьшения \Phi. Если \varphi_1>\varphi_2, то для минимума \Phi вся фаза 1 должна превратиться в фазу 2, и наоборот. Только в случае

\varphi_1(P,T)=\varphi_2(P,T)

возможно фазовое равновесие. Оттуда и до вывода формулы Клапейрона-Клаузиуса недалеко)

Отмечу, что

\left (\frac{\partial \Phi}{\partial P}\right)_T=V.

Для удельного потенциала V будет являться удельным объёмом вещества v. Рассмотрим жидкость под давлением P_{liq} в равновесии с её паром с давлением P_{vap}. Так как для двух фаз \varphi_{liq}=\varphi_{vap}, то рассмотрим их малые изменения при постоянной температуре. Получим

\left (\frac{\partial \varphi_{liq}}{\partial P_{liq}}\right)_T dP_{liq}=\left (\frac{\partial \varphi_{vap}}{\partial P_{vap}}\right)_T dP_{vap},

или же

v_{liq}dP_{liq}=v_{vap}dP_{vap}.

Теперь введу предположение, что пар - идеальный газ. Тогда v_{vap}=1/\rho_{vap}=(RT)/(\mu P_{vap}), и

v_{liq} dP_{liq}=\frac{RT}{\mu} \frac{dP_{vap}}{P_{vap}}.

Проинтегрирую это выражение и избавлюсь от никому ненужных индексов:

\Delta P = \frac{\rho RT}{\mu} \ln \frac{P}{P_0},

и, наконец-то (!):

P=P_0\exp \frac{μ\Delta P}{ρRT}.

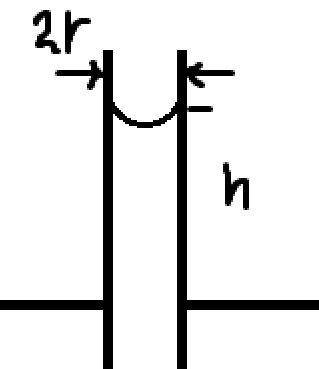
Осталось положить \Delta P = 2\sigma/r.

[Anton (Anton Morgunov)]

Мое увожение!

@Alisher

Теперь введу предположение, что пар - идеальный газ

Я могу предположить, что можно пойти дальше и сказать: допустим, что неидеальный газ можно описать с помощью некой величины так, что хоть pV \neq nRT, пусть эта новая величина f будет подчиняться интегральной форме \Delta X = RT \ln f_1/f_o . А если окажется, что эта величина f имеет линейную зависимость от p, то формула вообще будет применима для любых газов.

Просто я однажды задавался вопросом почему мы используем уравнения типа \mu_i = RT \ln p_i для любых газов, если ее вывод основывается на уравнении идеального газа. И ответ был ок, давайте вместо p_i введем некую фугитивность, так, чтобы это уравнение по прежнему работало. Математически строгих доказательств не видел, но вроде работает)

[Alisher (Alisher Yerkebayev)]

Ну вообще, если полагать, что насыщенный пар соответствует модели сплошной среды, а разность высот (в первом выводе формулы) не слишком велика, то формула принимает вид:

\Delta P = \frac{v_ж}{v_п-v_ж}\sigma K,

где v_п и v_ж – удельные объёмы пара и жидкости, K – кривизна с размерностью, обратной длине. То есть v_п в общем случае есть некая функция от P и T, но к тому же использование модели неидеального газа очень сильно усложняет конечную формулу. Хотя с величиной f вполне можно что-нибудь получить, спасибо за информацию)