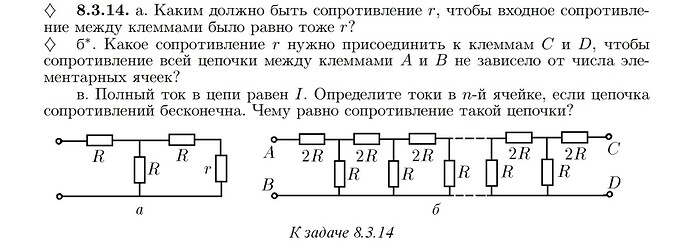
Полный ток в цепи равен I. Определите токи в n-й ячейке, если цепочка
сопротивлений бесконечна. Чему равно сопротивление такой цепочки?
1 лайк
Рисунок?
2 лайка
Рекомендую разобрать Задачу 12 этой книги.
2 лайка
Вспомни, к примеру, геометрическую прогрессию
b_{n+1} = b_n\cdot q.
Эта прогрессия, в своей сущности, является линейным и однородным рекуррентным соотношением. Поэтому общее его решение подбирается в виде степенной зависимости
b_n = b_0\cdot q^n.
Почему это так работает? Если подставишь второе уравнение в первое, то у тебя всё сократится, а значит второе уравнение действительно является решением заданного рекуррентного соотношения.
Теперь попробуем это сделать с рекуррентным соотношением (3):
\varphi_{k+1}=\left(2+\frac{R_1}{R_2}\right)\varphi_k - \varphi_{k-1}.
Как будет это в дальнейшем показываться, одинаково правильно будут работать как решение \varphi_k = \lambda^k, так и решение \varphi_k=\lambda^{-k}. Попробуем первое решение подставить. Выйдет
\lambda^{k+1}=\left(2+\frac{R_1}{R_2}\right)\lambda^k - \lambda^{k-1}\quad\Rightarrow\quad \lambda^2=\left(2+\frac{R_1}{R_2}\right)\lambda - 1.
Теперь подставим второе решение:
\lambda^{-(k+1)}=\left(2+\frac{R_1}{R_2}\right)\lambda^{-k} - \lambda^{-(k-1)}\quad\Rightarrow\quad 1=\left(2+\frac{R_1}{R_2}\right)\lambda - \lambda^{2}.
Как видишь, для обоих случаев эта подстановка сводится к решению квадратных уравнений, где \lambda определяется однозначно. А раз уж мы можем определить \lambda, то значит подбор степенной зависимости оправдан. В задачнике ещё показано, что в зависимости от знака перед дискриминантом, оба возможных решения \lambda_{1,2} взаимно обратны, т.е. \lambda_1 = 1/\lambda_2, что и оправдывает использование второго решения \varphi_k=\lambda^{-k}. Всё это говорит о том, что справедливо также взять и сумму решений \varphi_k = A\lambda^k + B\lambda^{-k}, коэффициенты A и B которого определяются начальными условиями (уравнение (7) в книжке).
Дополнение
В дополнении к тому, почему вообще можно использовать уравнение (7), добавлю, что “любая линейная комбинация решений также является решением этой системы” используется для точного описания очень многих физических явлений, подчиняющихся линейным законам.
Ты можешь элементарно вспомнить про принцип суперпозиции в электростатике, где электрическое поле в пространстве равно векторной сумме электрических полей от каждого заряда. Температурное распределение в материале является линейной суммой температурных распределений, создаваемых каждым источником тепла (всё благодаря тому, что в простейших случаях закон теплопроводности Фурье линеен). Электромагнитные, звуковые и т.д. волны, что подчиняются линейному волновому уравнению, могут линейно накладываться друг на друга без сторонних возмущений. Подобных примеров очень много.
И, наконец, добавлю про линейное дифференциальное уравнение движения механического тела, связанного “пружиной” (а точнее – любой линейной возвращающей силы F=-kx) в вязкой среде (сила сопротивления зависит от скорости движения тела), под действием гармонической силы:
\ddot x + 2\delta \dot x + \omega_0^2 x = f\cos\Omega t.
Существует частное решение вида x(t)=A\sin\Omega t + B\cos\Omega t, который в физическом смысле является установившимся движением тела. Можно продифференцировать, подставить, собрать всё по соответствующим “синусам” и “косинусам”, и тогда можно однозначно определить коэффициенты A и B.
Но мы ещё знаем, что если по правой части нашего дифференциального уравнения стоял бы 0 (то есть \ddot x + 2\delta \dot x + \omega_0^2 x = 0), то решением было бы
x(t)=Ce^{-\delta t}\cos(\omega t+\varphi).
А что же, в таком случае, будет, если в диффуру подставить сумму решений
x(t)=A\sin\Omega t + B\cos\Omega t + Ce^{-\delta t}\cos(\omega t+\varphi)?
А всё просто: при подстановке третье слагаемое (так называемое однородное решение) само собой сократится в нуль, а для первых двух слагаемых можно всё так же, без изменений, находить коэффициенты A и B. То обстоятельство, что общее решение линейных уравнений (будь-то рекуррентные соотношения или дифференциальные уравнения) является “частным решением” + “однородным решением”, было описано в §127 третьего тома Сивухина более непонятным языком (всё в его духе):
Не бойся, если математический приём “взятия с фонаря рандомного решения”, а также “суммирования этих рандомных решений” выглядит непонятным и каким-то слишком специфичным – он имеет множество применений, некоторые из которых я вынес в “Дополнение”. Поэтому обязательно запомни ту штуку, о которой ты спросил, подобные задачи со схожим методом решения не один раз будут всплывать в курсе общей физики.
9 лайков
Brilliance 
1 лайк