Шероховатая тяжелая стена движется так, что ее скорость составляет угол θ1 с собственной плоскостью. Скорость мяча составляет угол θ2 с плоскостью стенки. Если мяч не вращается до и после удара, найти связь между θ1 и θ2. Предположим, что углы θ1 и θ2 являются наименьшими углами между плоскостью стенки и скоростями. Столкновение упругое. дано, что после столкновения мяч движется перпендикулярно своей начальной скорости.
Please provide a solution, preferably in english!
in the wall’s inertial frame, it is obvious that the ball’s velocity is perpendicular to the wall’s surface (prove it)
1 лайк
I thought of this but i am unable to do so… the question has not given any data regarding masses, or velocities’ value… please explain in detail if possible with proof
Well, yeah, I guess there’s not enough data in the task. Denoting \hat \tau as basis vector along the plane of the wall (and \hat n perpendicular to it), the tangential change of momentum in wall’s frame of reference equals
\Delta \vec p = m(\vec v' \cdot \hat \tau) - m(\vec v_0 \cdot \hat \tau), \\ J\Delta \omega = \Delta p R = 0, \quad \text{thus} \quad \vec v' \cdot \hat \tau = \vec v_0 \cdot \hat \tau,
and the last thing implies the conservation of projection of velocity onto a plane. From conservation of energy we also get |\vec v'| = |\vec v_0|, thus \vec v\cdot \hat n = -\vec v_0 \cdot \hat n. This is the simple “light beam reflection” law, but it does happen when a friction force doesn’t occur, i.e. in this case we get \vec v_0 \cdot \hat \tau=0, so \vec v_0 is perpendicular to the wall in its reference frame. But if wall’s velocity in lab frame equals \vec V and ball’s velocity is \vec v, then we have
\vec v_0 = \vec v -\vec V, \quad \rightarrow \quad \vec v_0\cdot \hat \tau = \vec V\cdot \hat \tau - \vec v\cdot \hat \tau = 0, \\ \text{or} \quad V\cos \theta_2 = v\cos \theta_1.
As we can see, the relationship primarily depends on initial velocities too.
4 лайка
But the question says that only this much data is sufficient… so i guess we have to make some assumptions??
i think that authors simply forgot to introduce more data
2 лайка
Oh yeah it might be the case. Can we assume velocity/mass of the wall is so big that after collision, there is no effect on the walls velocity? Have you taken friction force into account?
the wall is “rough and heavy”, so its mass is big enough so there won’t be any effect on its velocity. the friction force changes the \hat \tau-projection of momentum, so I implicitly considered it through the change of momentum, but it equals zero because there’s no angular rotation.
2 лайка
Oh okay…, thanks a lot! I’ll ask if i get any further doubts.
One more doubt, what does the line- “Let us assume that the angles θ1 and θ2 are the smallest angles between the wall plane and the velocities” mean??
the angle can equally be either \theta or 180-\theta, but we euse the smallest value
1 лайк
Oh,ok
Alisher, what have you used the terms v’ and V and v0 for in the solution? I am a bit confused in the usage and it is bit confusing as in what term is used for initial velocity and final velocity etc.
v_0 and v’ are the initial and final velocities of the ball in wall’s frame, v and V are the velocities of ball and wall in lab frame respectively 
1 лайк
Thank you, I sent this to my professor, he is still saying that the question can be solved without use of velocity in the final expression. I don’t know how to proceed??
He has said that your solution is correct but it can be done without velocity expression in final answer. The final equation will be purely in form of θ1 and θ2
ok, i’ll think of it a little bit later
1 лайк
Yeah, thank you Alisher. You have helped me a lot, not only in this problem but in the other problems as well! I cannot express in words how much I appreciate your help, kind friend! This Beyond Community is really the best physics community I have found till now.
5 лайков
one more thing I want to add to the question, it is given the ball moves perpendicular to its initial velocity after collision. Now how can we proceed??
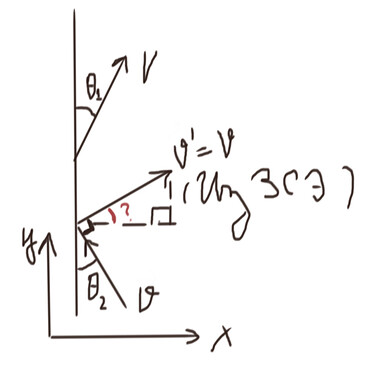
@Alisher а если так представить систему, то чему будет равен красный угол? Если его можно найти, то ведь достаточно расписать зси на ось и получится вывести связь между углами.