Вертикальное движение мячей

[sunrise]

1. Мальчик бросает вертикально вверх мяч. В момент, когда мяч достиг максимальной высоты,
   мальчик бросает вертикально вверх второй мяч, с того же места и с той же скоростью, что и первый.
   В результате мячи столкнулись на высоте H от места броска. Сопротивление воздуха не учитывать.

1. Найти время полета второго мяча до столкновения.
2. Найти начальную скорость мячей.
3. Какой путь прошел первый мяч до столкновения?
   Решение посмотрел, но ничего не понял (как всегда)

[ernur045 (Yernur Kairollayev)]

Ну я так полагаю, вы разбирали это решение, да тут проблемно что ничего не объясняется и есть небольшая опечатка. Так что будем его разбирать

Итак, первое что тянется сделать рука — нарисовать, а то какие-то точки, сразу и не представишь.

Где находятся точки А, В, С представили, теперь что за t_{AC} = t_{BC} = \tau? Первое — время, за которое второй мячик летит до точки столкновения, правая часть формулы — время, за которое первый мячик долетел до максимальной высоты и упал вниз до точки С.

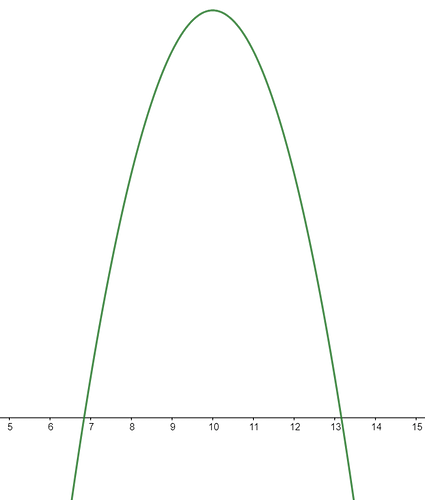
Чтобы понять следующую формулу, нужно понимать как работает движение с постоянным ускорением. Если нарисовать график подъема от времени, то получится парабола, которая выглядит как-то так (сорри, забыл числа в геогербре убрать, они никак не связаны с задачей):

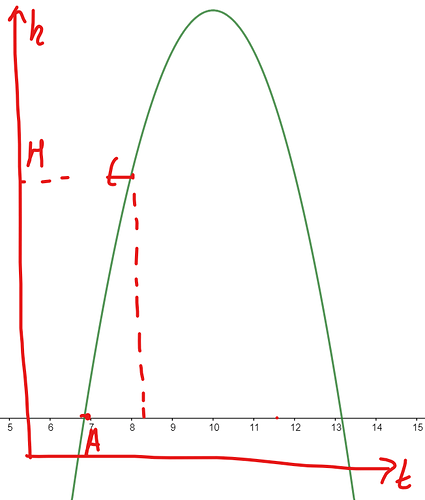
с максимумом при t = t_{AB}. Парабола — штука симметричная относительно максимума. Теперь отметим точки на ней

Для первого мячика

И для второго

А так как H равны для обоих графиков, и они симметричны относительно вертикальной прямой проходящей через точку B, значит поднимаясь от H до H_{max}, мяч затратит такое же время, как и падая от высоты H_{max} до H. Отсюда выходит, что поднявшись до максимальной высоты и упав до высоты H, первый мячик затратил t_{ABC} = 3\tau (вот тут лучше остановиться и ещё пару раз прочитать ответ, посидеть, подумать, порисовать, потому что это очень важная часть понимания движения с постоянным ускорением).

Дальше они просто подставляют эти значения для времени в формулы движения с постоянным ускорением

@sunrise

Решение посмотрел, но ничего не понял (как всегда)

Лично у меня, если я не понял решение, я прихожу к выводу, что недостаточно сидел над задачей. Либо же я просто не понял систему и нужно вместе с автором понимать, а это сложнее, так как обычно (из тех, что я заметил) решения пишутся, чтобы помочь найти тот момент, который вы упустили при решении задачи. Над каждым предложением (или формулой) нужно сидеть и думать, пока не поймёшь его полностью и не подумаешь зачем оно нам нужно в этой задаче