Collision with thin rod

Физика Механика
1

A thin rigid rod with negligible mass and length \ell is connected to a mass point of mass m_1, m_2 at its two ends, and it is placed at rest on a smooth horizontal surface. A particle with mass m collides with a m_2 particle in the direction of the angle \theta with the thin rod at initial velocity v_0, as shown in the figure. It is known that the velocity directions of m and m_2 before the collision are on the line connecting the two particles, so the velocity direction of the incident particle m after the collision is still on the straight line of the original velocity direction. This question assumes that all collisions are perfectly elastic collisions, please answer the following questions:
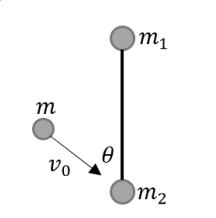
Screenshot (2308)

  1. What is the direction and magnitude of the velocity \vec{v} of the incident particle m immediately after the collision?
  2. What is the direction and magnitude of the velocity \overrightarrow{v_1} of the particle m_1 immediately after the collision?
  3. Discuss the impulses exerted on the thin rod by the mass points at both ends of the thin rod at the moment of collision, and calculate the sum of the impulses on the thin rod.
  4. Please prove that the impulse transmitted by the thin rod is always along the direction of the thin rod (there is no vertical thin rod component).
  5. If m_1 is at rest immediately after the collision, can it be considered that m and m_2 complete the elastic collision first without being disturbed by m_1? What are the conditions when this happens? Please use the result of (2) to discuss quantitatively.
1 лайк
2

It doesn’t really seem like a difficult problem. Do you have any attempts or ideas?

1 лайк
3

Yeah I was typing my answer, I wanted to match it. I am getting the answer of (1) as:

v=\frac{\left(m_1+m_2\right)-m\left(\frac{m_1}{m_2} \sin ^2 \theta+1\right)}{\left(m_1+m_2\right)+m\left(\frac{m_1}{m_2} \sin ^2 \theta+1\right)} v_0
5

Your answers should be correct if you used the conservation of angular momentum L=const, conservation of energy E=const and the conservation of linear momentum p=const correctly. I truly believe that you don’t really need help that much, 'cause you must have studied the collisions where the body will rotate, but if you have questions or if something is not understandable to you, then you’re welcome. Take into account that the bodies with masses m_1 and m_2 will rotate relative to the center of mass the position of which you can find by using \vec r_{CM}=\frac{\sum m_i\vec r_i}{\sum m_i} and the velocity of the center of mass \vec v_{CM}=\frac{\sum m_i\vec v_i}{\sum m_i} and the center will itself move.

2 лайка
6

Thanks!