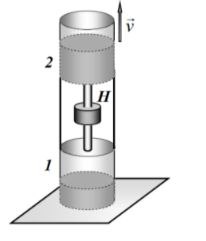
На электронные весы установили модель насосной станции: два одинаковых бака 1 и 2 закреплены вертикально, один над другим. Баки частично заполнены водой, плотность которой равна \rho, площадь поперечного сечения баков равна S. Баки соединены трубой с насосом H. При отключённом насосе (и неподвижной воде) весы показывают значение \mu_0. После включения насоса вода стала перекачиваться из нижнего бака в верхний, при этом уровень воды в верхнем баке поднимается с постоянной скоростью v.
- Чему равно показание весов \mu_1 в процессе перекачки воды насосом из верхнего бака в нижний с той же скоростью v
Решение вижу так:
Mx_c = M_0x_0 + \rho S h_2 (l + \frac{h_2}{2}) + \rho S h_1 \frac{h_1}{2}
h_2 = h_0 - vt
h_1 = vt
Где:
M_0 - масса системы без воды
x_0 - центр масс системы без воды
l - расстояние до дна второго бака
Решаем, находим 2 производную по t:
Ma_c = 2 \rho S v^2
Применяем 2 ЗН:
N - Mg = Ma_c
N = \mu_0(1 + \frac{2 \rho S v^2}{\mu_0}) - ответ вроде даже сошелся. Получил полный балл за задачу.
Собственно вопросы:
-
За счет какой внешней силы движется ЦМ? За счет силы которую создает насос? Т.е. на систему действуют внешние силы: сила тяжести, сила реакции опоры и сила которую создает насос. Но если так, то почему эту силу мы не учитываем во 2 законе Ньютона для системы. Если это внутренняя сила, то получается что ЦМ перемещается под действием сил N и Mg.
-
Когда вода перекачивается из верхнего бака в нижний, то по логике получается что координата ЦМ системы перемещается вниз (значит и ускорение направленно будет вниз). Но из уравнения видно, что усорение ЦМ системы направлено вверх.