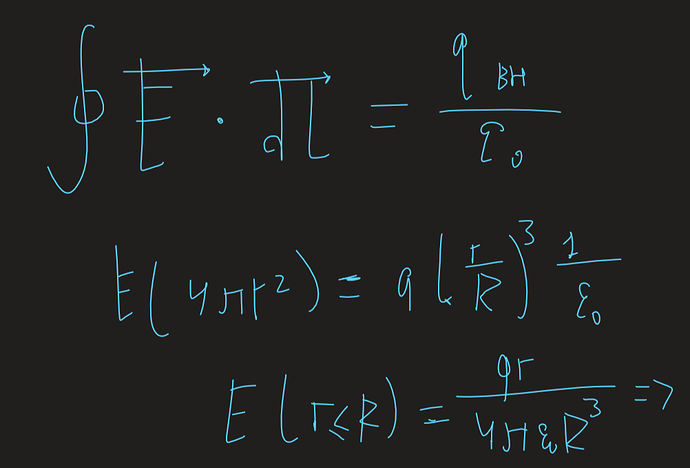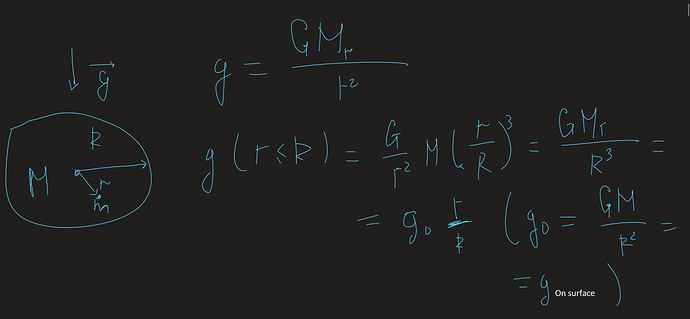Решал эту же задачу, только вместо потенциала напряжённость поля?
Да, решал
1 лайк
Вроде с теоремой Гаусса можно сделать, то что вы сказали
1 лайк
Вроде когда заряд распределён по объёму его можно считать сконцентрированным в одной точке. Или когда по поверхности? Я забыл
1 лайк
Почему это так?
Из-за индукции заряда, симметрии. Об этом лучше прочитать в Джанколи 22-25 главы (фулл электростатика)
1 лайк
В общем, одна из главных, так сказать, проблем потенциала в том, что нам нужно задать какую-то точку, в которой потенциал будет равен нулю. Потому что потенциал обычно находят как интеграл напряжённости, а когда мы считаем интеграл всегда вылезает константа интегрирования. Даже когда мы просто задаём значение потенциала или находим его прибором, мы задаём его относительно какой-то точки. Потому что такова природа потенциала.
Как правило, в задачах нулевой потенциал либо задан, либо достаточно сказать что потенциал на бесконечности равен нулю.
Сорри, мне что-то сложно понять, что здесь происходит
Да
Всегда беспроигрышным вариантом будет использование определения потенциала
\varphi = - \int _a^b \vec E \text d \vec l = - \int _a^b E \text d l \cdot \cos \alpha
\alpha — угол между векторами \vec E и \vec l
3 лайка
Когда у нас равномерно заряженная сфера или шар мы можем считать, что весь заряд в центре. Однако, нельзя это применять когда мы ищем поле внутри сферы/шара
2 лайка
Почему нет?
Ну используя ту же теорему Гаусса. Сравни поле внутри шара если допускать, что весь заряд шара сосредоточен в центре и если учитывать, что он распределён равномерно
Так мы ведь берём не весь заряд шара, а только тот, который в пределах r
Ну да. Я к тому что мы не можем сосредоточить весь заряд шара в центре, в таких ситуациях
1 лайк
Пункт а вроде решено правильно.
Если что пункт б можно решить так:
Воспользуемся теоремой Гаусса, для оболочки радиусом r, внутри шара: (учитывая при этом, что заряд на оболочке пропорционален его радиусу в кубе - объему)
Для того, чтобы найти потенциал внутри шара как функцию r, воспользуемся тем фактом, что вектор напряженности является антиградиентом (градиентом с минусом) потенциала: (здесь нужно немного интегралить как говорит обычно @ernur045 )
У нас появилась константа в интеграле, которая по своему смыслу является потенциалом в центре шара. Константу, то есть потенциал в центре можно найти зная потенциал шара на его поверхности (в этом случае заряд шара можно рассматривать точечным и сосредоточенном в центре)
Отсюда потенциал в центре шара:
Следовательно потенциал внутри шара как функция r:
Вообще эта тема довольна интересна. Можно применить эти же принципы в гравитации:
(здесь роль напряженности будет играть ускорение свободного падения)
Пользуясь теми же принципами, что и в электростатике находим g на поверхности:
Учитывая, что сила - антиградиент потенциальной энергии:
Опять же, константа выражает потенциальную энергию в центре:
Это кстати можно доказать используя solid angles (телесные углы):
Рассмотрим произвольную точку Р, где находится точечная масса m, и которая расположена на расстоянии r от центра шара
Телесные углы, приведенные на рисунке одинаковы (они вертикальны):
Используем определение телесного угла:
Выразим силы со стороны 1 и 2 части земной коры:
Отсюда видно, что модули сил равны, но векторы направлены противоположно, поэтому суммарная сила равна нулю. Исходя из этих соображений можно сделать вывод о том, что результирующая сила части земли за пределами радиуса r равна нулю, поэтому рассматривается только внутренняя часть. Те же принципы можно применить к электростатике и доказать, что там тоже рассматривается только внутренняя часть
3 лайка