Как доказать принцип Ферма при преломлении света без использования производной?
Я так понял, надо доказать закон Снелла через принцип Ферма? Если да, то не знаю насчет принципа Ферма, но можно доказать этот закон другим способом, без использования производной. Доказывается с помощью принципа Гюйгенса (я не особо разбираюсь, поэтому возможно они как-то взаимосвязаны).
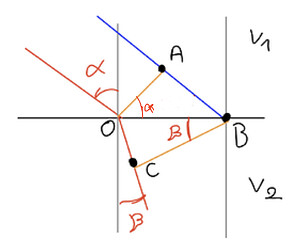
Для начала построим следующую модель:
Положим, что красный и синий лучи были излучены одновременно. В тот момент, когда красный луч достигает точки О, синий луч достигает точки А. Скажем, что когда синий луч достигает точки В из точки А, проходит время \Delta t. За этот промежуток времени, красный луч достигнет точки С из точки О. По принципу Гюйгенса,
||\vec{OC}|| = v_2\Delta t ; \ ||\vec{AB}|| = v_1\Delta t
Геометрически можно заметить, что ||\vec{OB}|| = \dfrac{||\vec{OC}||}{\sin \beta} = \dfrac{||\vec{AB}||}{\sin \alpha}. Другими словами,
\frac{v_2\Delta t}{\sin \beta} = \frac{v_1\Delta t}{\sin \alpha}
Отсюда и получается, что
\frac{\sin \alpha}{\sin \beta} = \frac{v_1}{v_2} = \frac{n_2}{n_1}
9 лайков
Спасибо большое но я имел ввиду:
По принципу ферма время t из рисунка выше должно быть минимальным значением,но здесь они использовали производную
Можно ли найти минимум этого выражения без производной?
1 лайк
В чём проблема начинать учиться пользоваться производными?
10 лайков