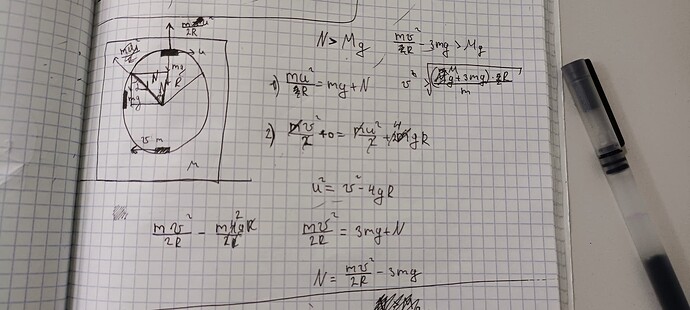
Тело представляет собой куб, в котором вырезана сферическая полость радиуса R. Внутри сферыческой полости в нижней точке покоится шайба, геометрическими размерами которой можно пренебречь. Найдите минимальную горизонтальную скорость (при всех возможных отношениях масс куба и шайбы), которую необходимо сообщить шайбе, чтобы в процессе движения куб оторвался от поверхности стола. Трение в системе полностью отсутствует. При каком отношении масс куба и шайбы M / m достигается минимальное значение скорости шайбы?
Вот мое решение я взял что куб приподнимется когда шайба будет на самом верху полости,правильно ли я сделал можете подсказать?(ответ не правильный)
4 лайка
Учитывай, что сам куб может свободно скользить по поверхности. Здесь выполняется ЗСИ системы на горизонтальное направление
3 лайка
Попробуй записать закон сохранения импульса. Начальный импульс = Конечному импульсу. То есть, когда шайба будет в верхней точке, скорость будет направленна вправо => куб будет двигаться влево, так как силы трения нет.
-
Ты должен пересесть в СО куба, что бы легче решить задачу)
А если ты будешь решать в Земной системе отсчета, то радиус кривизны не равен R. Это и есть твоя ошибка. Пересядь в СО куба, в этом случае радиус кривизны будет R. -
Запиши закон сохранения энергии
-
В верхней точке N+mg=(mVотн^2) / R.
Ты правильно написал условие отрыва: N\geq Mg
По сути этого должно хватить чтобы решить данную задачу
8 лайков