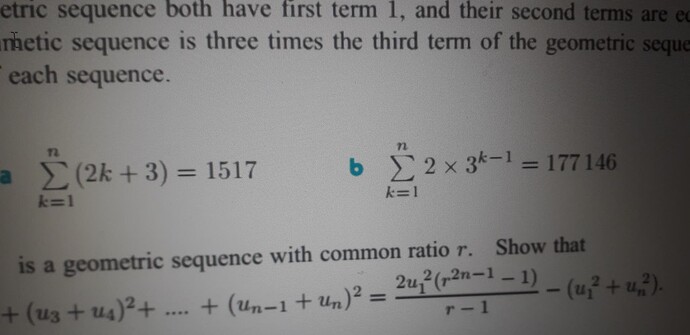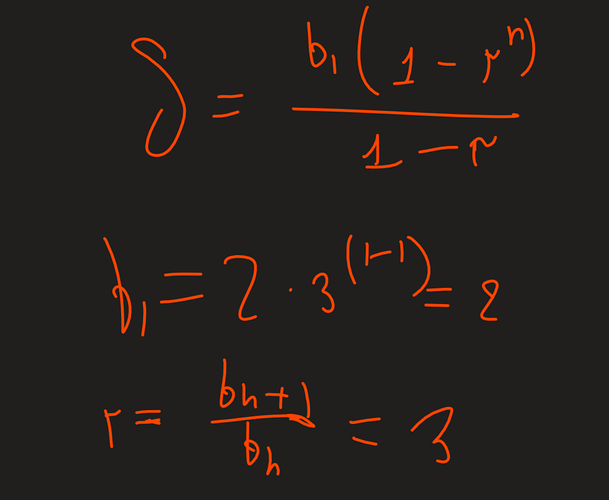Математика 11 класс. Нужно найти число n

[Ashimov_Assanali]

[Damir (Yekibayev Damir)]

Используй формулу для суммы до n-го члена геометрической прогрессии: S=b1(1-r^n)/1-r

[Ashimov_Assanali]

Я не понял ваше решение

[Alisher (Alisher Yerkebayev)]

например, решим пункт a)

Последовательность 2k+3 является рядом нечётных чисел, начиная с 5, т.е. 5, 7, 9, ... . Тогда их сумма представляется в виде

\sum_{k=1}^{n}(2k+3) = 5+7+9+11+...

Этот ряд образует арифметическую прогрессию, где каждый последующий член больше предыдущего на d=2. Пусть первый элемент последовательности a_1=5, тогда сумма членов арифметической прогрессии высчитывается по формуле

S_n=\frac{2a_1+d(n-1)}{2}n = \frac{2\cdot 5 + 2(n-1)}{2}n=1517

Немного преобразований, и выясняется, что достаточно решить квадратное уравнение

(n+4)n=1517.

Подобным образом и решается геометрическая прогрессия. Первый член равен b_1=2, а знаменатель этой прогрессии q=3, а сумма прогрессии высчитывается по формуле, что писал @Damir:

S_n = b_1\cdot\frac{q^n-1}{q-1}

[byeadeal]

Первое можно так же решить через закономерность суммы последовательных нечетных чисел
1+3=2^2
1+3+5=3^2
1+3+5+7=4^2 и так далее
Теперь,мы тогда можем преобразовать наше уравнение следующим образом:
n^2-4=1517 (4 вычли,так как счет начинается с 5)
отсюда n^2=1521,где n=39.Однако,стоит не забывать,что это сумма с 1 и 3,а в начальной их не было,тогда нам нужно вычесть 2 из 39,чтобы найти количество всех членов в сумме
Ответ:n=37