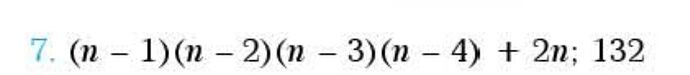Есть ли какие то ограничения на последовательность? 2, 4, 6, 8, 34 ни OEIS, ни вольфрам не находит ![]()
a_1=2, a_5=34
Я решил но с помощью Матрицы и вышло
Просто хотелось узнать есть ли более быстрый метод.
В ответе она в более красивом виде
Во первых, несложно заметить, что первые 4 члена данной последовательности это члены последовательности 2n, а пятый член нет. Отсюда можно просто подогнать, сказав, что a_n=k\cdot f(n)+2n, где f(n) это какая-нибудь функция, которая в точках n= 1, 2, 3, 4 будет равна нулю, а в точке n=5 будет ненулевой, а потом просто подобрать k так, чтобы k\cdot f(n) было равно 24. Ну и самая лёгкая функция, которая может прийти в голову, удовлетворяющая данным условиям это f(n)=(n-1)(n-2)(n-3)(n-4). Причём всё так идеально совпадает, что ещё и k в таком случае оказывается равной единице.
А это точно математика?)))
Самый легкий метод - использовать интерполяцию Лагранжа. Ваше решение по сути как раз таки это и делает. Значения x_i это 1, 2, 3, 4, 5, а значения y_i это 2, 4, 6, 8, 34.
Интерполяция Лагранжа - одно из обязательных знаний для олимпиадника по математике.