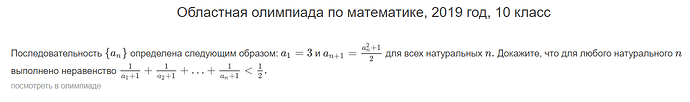Помогите пожалуйста решить задачу, описать метод и идею решения. Как додуматься до того или иного шага? Буду очень признателен вам, если поможете)
Я бы предложил следующую идею: найти функцию f(n), такую что:
i)f - возрастает
ii)\sum_{i=1}^{n} \frac{1}{1+a_{i}} < f(n) < \frac{1}{2}
то есть как бы зажать ее между частями неравнества
и придется доказать уже другое неравенство \sum_{i=1}^{n} \frac{1}{1+a_{i}} < f(n), которое уже больше похоже на решаемое
по моему на матоле есть решение этой задачи. все ли ясно с тамошим решением?
я так понял автор хочет подсказок (чтобы была возможность добить самому), а не сразу полного решения
Пусть
Тогда попробуй найти такое f(k) > 0, что S_{k} = \frac{1}{2} - f(k).
Решение отличное от матольного, в принципе на матоле тот же принцип найти f(n) и доказать что оно зажимается между левой и правой частью (ток это решение более ественственное, считаю, но по технике довольно муторная Трипл индукция )
Возьмем самую простую f(n): \displaystyle{\lim_{n \to \infty}f(n) = \frac{1}{2}} и f - строго возрастает (это по идее и обозначает условие ii), и ею будет f(n)=\frac{n}{n+1} \cdot \frac{1}{2}. Несложно заметить, что f(n) < \frac{1}{2}
Осталось показать) что \displaystyle\sum_{i=1}^{n} \frac{1}{a_{i} + 1} < f(n), \forall n \in \mathbb{N}, покажем по индукции
У нас будет доказать неравентство вида a_{n+1} > P(n), при достаточно больших n, где P(n) - многочлен второй степени - его мы тоже покажем по индукции.
Мы сведем индукцию выше к доказательству неравенства Q(n) > R(n), при достаточно больших n, где Q(n), R(n) тоже многочлены - его мы тоже покажем по индукции((
Идея заключается фактически в переходе неравенств содержащих a_{n} и n к неравенствам содержащие чисто n, при помощи многократного применения индукции, а такие неравенства в данном случае имеют вид: многочлен против многочлена