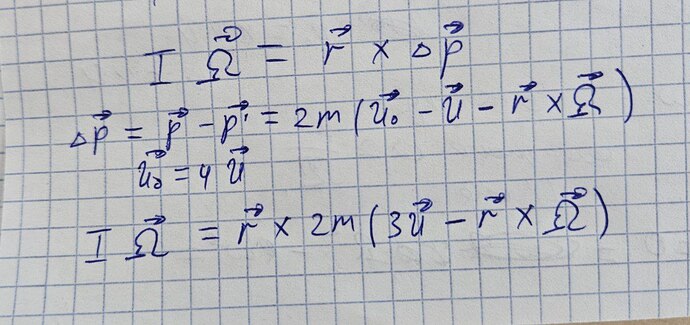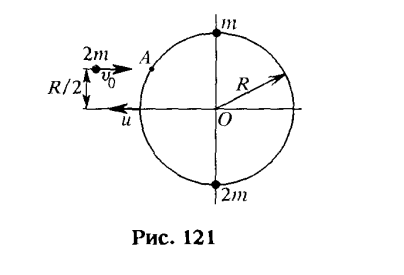
6.12. По гладкой горизонтальной поверхности поступательно без вращения движется система, состоящая из двух массивных шариков, плотно насаженных на проволочное кольцо (рис. 121). Массы шариков m и 2m, радиус кольца R. Навстречу кольцу движется пластилиновый шарик массы 2m со скоростью v_0 , параллельной вектору скорости системы. Шарик сталкивается с кольцом и прилипает к нему в точке А на расстоянии R/2 от диаметра, вдоль которого двигалась система до удара. Пренебрегая массой проволочного кольца и трением о поверхность, найти угловую скорость вращения системы \omega после удара, также скорость u, с которой двигалось кольцо, если известно, что центр инерции системы движется в обратной направлении с той же скоростью u.
верно ли я записал изменение момента импульса системы?