3 лайка
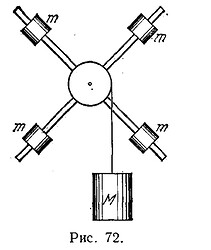
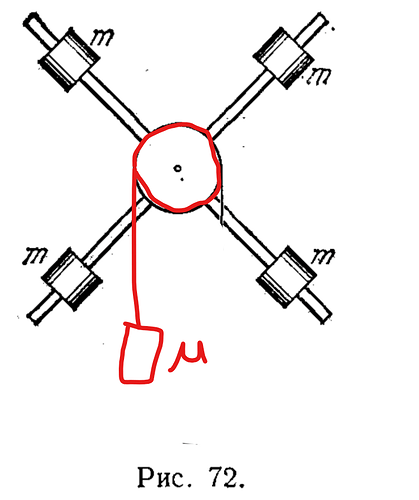
Ну шкиф и крест Обербека симметричный, поэтому массы в кресте никак не влияют.
Вот у тебя есть 2 уравнение:
Ma = Mg - T\\
\frac {d(I \omega)}{dt} = (Mg -T)r
Эти уравнение “принадлежат” к динамике, но тут у нас сложное движение, состоящее из вращения и поступательного движения груза. Значит, нам нужно какое-то уравнение, которое связывает эти два движения. Нить по шкиву не проскальзывает, поэтому пишем:
a = r \frac {d\omega}{dt}
Теперь у нас есть 3 уравнения 3 неизвестных, можно решать систему
Ещё одна важное дополнение к ответу, у уравнение для моментов записано не совсем верно. Прежде чем читать его, предлагаю вспомнить простейшую систему: два грузика на нерастяжимой нити, перекинутой через блок, и вспомнить, какая сила действует вдоль нити.
В чём ошибка
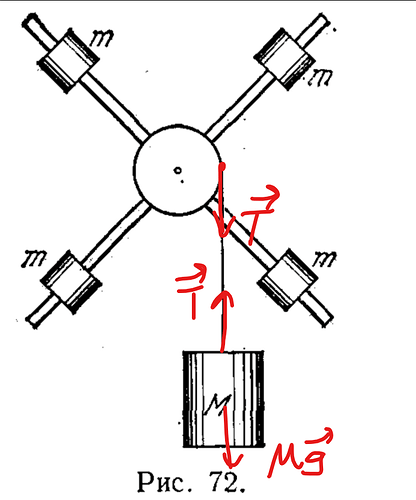
Вдоль нити всегда дейсвует сила T, если нить к чему-то прикреплена, она будет действовать с силой T. Поэтому как нить действует на груз с силой T, так и на шкиф она действует с силой T. Короче говоря, на шкиф действует нитка, а груз он связан с ниткой, а не со шкифом, поэтому нам нужно считать только действие этой нитки на него
Ну поэтому формула для моментов будет выглядеть так
\frac {d(I \omega)}{dt} = Tr
5 лайков
Можно написать закон сохранения энергии Mgh=\frac{Iw^2}{2}+\frac{Mv^2}{2}. Часть со скоростью я не понял. Почему на полуобороте импульс груза 2Mv?
Это же решение к вопросу про натяжение нити во время рывка?
Да, груз опускают на высоту h и происходит рывок наверх.
Направим ось Oy вверх. В начале груз имел импульс: p_0 = - Mv. Рывок можно считать абсолютно упругим, поэтому после рывка груз имеет импульс: p = Mv. И тогда изменение импульса: \Delta p = p - p_0 = 2Mv
1 лайк
Как поднимается груз? Почему у него скорость V, когда груз поднялся?
1 лайк
