1 лайк
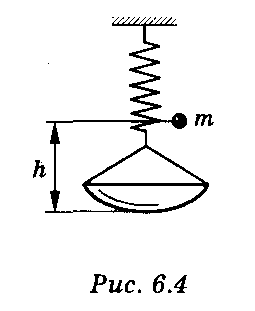
Через законы сохранения импульса при ударе и сохранения энергии в процессе колебаний вычисляешь амплитуду колебаний. Дважды дифференцируя уравнение гармонических колебаний x=x_0+A\sin(\omega t + \varphi) (неизвестные которого тебе предстоит вычислить), находишь ускорение груза \ddot x. В момент, когда это ускорение максимально, записываешь второй закон Ньютона для груза: m\ddot x=mg-N. Условие отрыва: N=0.
3 лайка
я нашел амплитуду но не могу дальше решить
Возьмём производную вышенаписанного уравнения с использованием цепного правила дифференцирования сложной функции (разбираю в подробностях)
\dot x = \frac{d}{dt}(x_0+Asin(ωt+φ) = A\cdot \frac{d(sin(ωt+φ))}{dt}
Теперь надо разделить и умножить полученное выражение на дифференциал d(ωt+φ). Таким образом мы можем взять производную из таблицы (\sin x)'=\cos x.
\dot x=A\cdot \frac{d(sin(ωt+φ))}{dt} = A\cdot \frac{d(sin(ωt+φ))}{d(ωt+φ)} \cdot \frac{d(ωt+φ)}{dt} = \newline = A\cdot \cos (ωt+φ) \cdot ω
Таким же образом берём производную во второй раз, чтобы получить ускорение груза:
\ddot x = -ω^2A\sin(ωt+φ)
Знак минус говорит о том, что если груз смещён вниз, то ускорение направлено в противоположную сторону и наоборот.
Теперь мы знаем уравнения для x, \dot x и \ddot x. Как определить коэффициенты? Подставлять для них начальные условия.
Частота ω определяется легко и не требует пояснений: ω=\sqrt {\frac{k}{M+m}}
Координата x_0 выбирается произвольно; можно взять как x_0, так и приравнять её к растяжению пружины из-за чашки, т.е. x_0=M/k.
В пределах данной задачи фазу φ находить необязательно, но она определяется подстановкой начальных условий в уравнения движения. Мы знаем, что в момент времени t=0 груз ударился о чашку, тогда \dot x(0) = v_0= ωA\cos φ, где v_0 – начальная скорость движения системы, которую ты определишь из законов сохранения.
Наконец, найдём условие отрыва груза:
m\ddot x =-ω^2A\sin(ωt+φ)= mg - N
Как видим, ускорение максимально тогда, когда \sin(ωt+φ)=-1, для него положим N=0. Значение синуса, взятое с минусом, говорит о том, что фаза колебаний будет равна (ωt+φ)=3\pi/2, то есть груз оторвётся от чашки в наивысшей точке их движения. Подставляешь все известные тебе значения и получаешь ответ.
Впредь рекомендую тебе прокачать свой мат. аппарат, чтобы научиться решать подобные и многие другие задачи. Выше я расписал практически всё, что нужно уметь для того, чтобы решать задачи на гармонические колебания, используй это, чтобы практиковаться на других задачах, так тема лучше усвоится.
5 лайков