Савченко 3.4.17*

Физика Механика
1

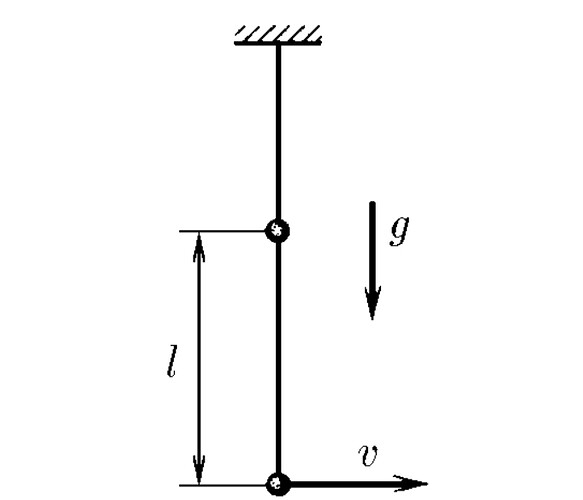
Собственные частоты двойного маятника равны ω1 и ω2. Длина нити, связывающей шарики маятника, равна l. В состоянии равновесия нижнему шарику сообщили небольшую скорость v. Определите максимальное отклонение нижнего шарика от положения равновесия и длину нити, связывающей верхний шарик с потолком.

IMG_8348
IMG_8348681×584 20.4 KB

Здравствуйте,могли бы вы подсказать как решить эту задачу?

2

Пусть 1 шарик - тот что повыше (все большие буквы), 2 - тот что пониже (маленькие)

Mg - T + t = 0
-T\Theta + t\theta = ML\ddot\Theta
mg -t = 0
-t\theta = m(L\ddot\Theta + l\ddot\theta)

Получаются два вот таких уравнения

(M+m)L\ddot\Theta + ml\ddot\theta + (M+m)g\Theta = 0
l\ddot\theta + L\ddot\Theta + g\theta = 0

Предпологая \Theta = A\sin\omega t, \theta = B\sin\omega t

A (M + m)(g-L\omega^2) - Bml\omega^2 = 0
Al\omega^2 + B(l\omega^2 - g) = 0

Получается линейная однородная система, решения которой
существует если определитель ее матрицы равен нулю

MlL\omega^4 - (M+m)(L+l)g\omega^2 + (M+m)g^2 = 0

По теореме Виета

\omega_1 ^2 + \omega_2 ^2 = \frac{(M+m)(L+l)g}{MlL}
\omega_1 ^2\omega_2 ^2 = \frac{(M+m)g^2}{MlL}

Отсюда находишь L и отклонение через уравнение движения (x = l\theta + L\Theta)

2 лайка