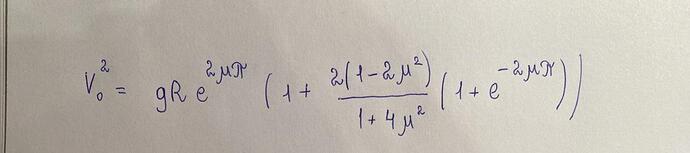Дана окружность радиуса R, которая закреплена к плоскости. В самой нижней точке этой окружрости находится маленькое тело. Какую минимальную, начальную скорость нужно приложить этому телу, чтобы оно ровно в самом верху оторвалось от окружности? Коэффициент трения тела об окружность равен μ. Силовая характеристика гравитационного поля g.
1 симпатия
Пока не знаю как получить ответ, но вот немного продвижения из уравнений динамики (угол \theta отсчитываю от нижней точки)
mR\ddot\theta=mR\dot\theta\frac{\text{d}\dot\theta}{\text{d}\theta}=\frac{mR}{2}\frac{\text{d}(\dot\theta^2)}{\text{d}\theta}=-mg\sin\theta-\mu(mg\cos\theta+m\dot\theta^2R)
\frac{1}{2}\frac{\text{d}(\dot\theta^2)}{\text{d}\theta}+\mu\dot\theta^2=-\frac{g}{R}(\sin\theta+\mu\cos\theta)
6 симпатий
решение
\dot\theta^2=\frac{2g}{R}\left(\frac{1-2\mu^2}{1+4\mu^2}\cos\theta-\frac{3\mu}{1+4\mu^2}\sin\theta\right)
вроде подходит под это уравнение, но я не задавал начальные условия
P.S. я угадал решение вида \dot\theta^2=A\cos\theta+B\sin\theta, подставил и решил систему уравнений относительно этих коэффициентов
upd. надо подобрать другое решение, полученное выше немного похоже на правду, но это не то
4 симпатии
итак, вот моё окончательное решение.
Это всё я по идее могу записать как
\dot y +2\mu y = \frac{2g}{R}\sqrt{1+\mu^2}\cos(\pi/2+\theta+\arctan\mu),
где y≡\dot\theta^2, \dot y ≡\text{d}y/\text{d}\theta,
и это очень похоже на диффуру для заряда конденсатора в цепи с источником синусоидального напряжения, резистора и конденсатора, т.е. общее решение этой штуки будет суммой частного решения (когда y меняется синусоидально) и решения однородного уравнения (правая часть равна нулю). Тут, конечно, колебаний и не будет)) но во всяком случае это просто соответствует приравниванию коэффициента при \ddot y нулю.
Итак, решаем однородное уравнение:
\dot y + 2\mu y = 0 \quad\rightarrow\quad y = Ce^{\displaystyle -2\mu\theta},
где C определяется заданием начальных условий
Значит, если для уравнения
\dot y + 2\mu y = \frac{-2g}{R}(\sin\theta+\mu\cos\theta)
подобрать решение вида
y = A\cos\theta+B\sin\theta + Ce^{-2\mu \theta}
то, во-первых, первые два слагаемых соответствуют моему выводу выше, а третье слагаемое зависит от того, какие величины мы будем подставлять. То есть для уравнения
\dot\theta^2=\frac{2g}{R}\left(\frac{1-2\mu^2}{1+4\mu^2}\cos\theta-\frac{3\mu}{1+4\mu^2}\sin\theta+ Ce^{-2\mu\theta}\right)
если подставить \dot\theta^2 = g/R для \theta=\pi, то получаем
C=\frac{1}{2}\frac{3}{1+4\mu^2}e^{2\mu\pi}
Следовательно, финальным ответом является
v_0^2 = (\dot\theta(0)\cdot R)^2= gR\left(\frac{2-4\mu^2}{1+4\mu^2} +\frac{3}{1+4\mu^2}e^{2\mu\pi}\right)
9 симпатий
Алиш привет, у тебя очень крутое решение) Если хочешь узнать ответ и решение, то спроси у Шатохи (Шатохин Даниил). Это он мне дал эту. Это очень круто, что ты решил её, некоторые её называют 9 кругов интегрального ада. Спасибо за решение))))!!!
1 симпатия
К сожалению, решение приведённое Алишером содержит ошибку. Это можно понять по тому, что при подстановке достаточно большого коэффициента трения в конечное выражение для ответа получается отрицательный квадрат скорости. Данную задачу можно решить другим методом, используя Метод Лагранжа при решении линейного дифференциального уравнения первого порядка полученного Алишером. Таким образом, получается ответ:
5 симпатий
я попробовал зависимость вывести этим методом и получилось точно так же. Просто в решении выше надо исправить
C=\frac{3}{2(1+4\mu^2)}e^{2\mu\pi}
6 симпатий
да это же просто эллиптический интеграл, ты этот ответ в таком интегральном виде оставляешь и норм
1 симпатия
Какой-то узкоспециализированный физический юмор
2 симпатии
Ну вот в химии вы же всегда по действиям находите значения, а далее используете округленные значение (по крайней мере нас так в школе учили). А вот представьте, если вывести одну конечную формулу, как в физике и получить более точное значение. Тут происходит примерно то же самое, только вместо химии — физика, вместо физики — математика
1 симпатия
это не настоящие химики, это дип фейки
1 симпатия