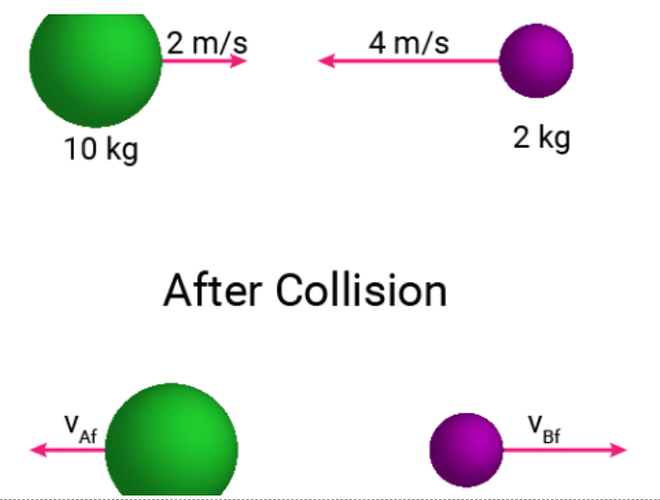
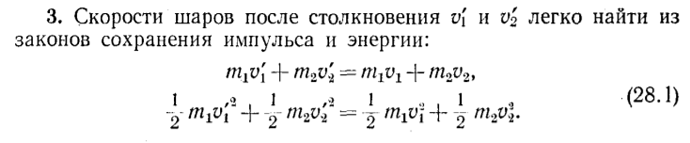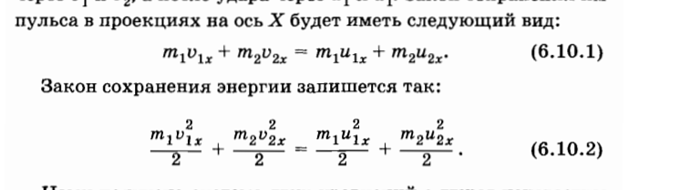Ну для начала стоит вспомнить, какие законы сохранения применимы в этой задаче. Elastic collision – упругое столкновение, в котором сохраняется импульс (как и почти во всех задачах на столкновения) и энергия.
Первое уравнение, закон сохранения импульса, ты записал правильно (надеюсь ты понимаешь почему именно такие знаки, потому что это часть в которой нередко возникают затруднения)
Со вторым уравнением возникли проблемы. Ты не можешь взять и просто возвести скорости в квадрат в законе сохранения импульса. Так можно делать только если v_1 = v_2 = v'_1 = v'_2, что является частным случаем, когда сталкиваются два одинаковых шарика с одинаковыми скоростями. Правильнее будет записать закон сохранения энергии
\frac {m_1v_1^2}{2} + \frac {m_2v_2^2}{2} = \frac {m_1 {v'_1}^2}{2} + \frac {m_2{v'_2}^2}{2}
То есть, суммарная энергия до столкновения равна суммарной энергии после столкновения.
В итоге у тебя получается система уравнений:
m_1v_1 - m_2 v_2 = -m_1v'_1 + m_2v'_2 \\
m_1v_1^2 + m_2v_2^2 = m_1 {v'_1}^2 + m_2{v'_2}^2
Дальше можно идти двумя путями:
-
“Влоб”. Из первого уравнения найдём v'_1 или v'_2 и подставим во второе уравнение и будем решать квадратное уравнение.
-
Использовать метод, который привёл Сивухин в своём учебнике, а потом удивлять учителей и одноклассников этим решением 
Перезапишем уравнения:
m_1 (v_1 + v'_1) = m_2(v_2 + v'_2) \space \space \space (1) \\
m_1(v_1^2 - {v'_1}^2) = m_2({v'_2}^2 - v_2^2)
По формулам сокращенного умножения (a^2 - b^2) = (a+b)(a -b):
m_1(v_1 - v'_1)(v_1 + v'_1) = m_2(v'_2 - v_2)(v_2 + v'_2)
Разделим получившееся уравнение на уравнение (1):
v_1 - v'_1 = v'_2 - v_2
И теперь у нас есть линейных уравнения: верхнее и уравнение (1). Выражаем в одном из уравнений v'_1 или v'_2, подставляем полученное выражение во второе и приходим к ответу.
Эту тему (как и многие другие из школьной программы по механике и термодинамике) очень хорошо объясняет Мякишев (тык)
P.S.: Чтобы поставить знак умножения в \LaTeX , можно использовать команду
\cdot
Результат: a \cdot b
P.P.S.: советую привыкнуть работать с буквенными уравнениями, потому что большинство учебников и задачников используют именно этот метод. Ещё так гораздо понятнее, что происходит в системе, и общем удобнее запоминать методы.