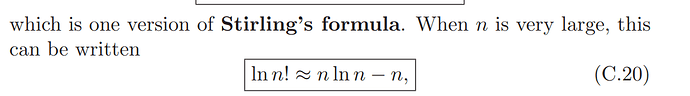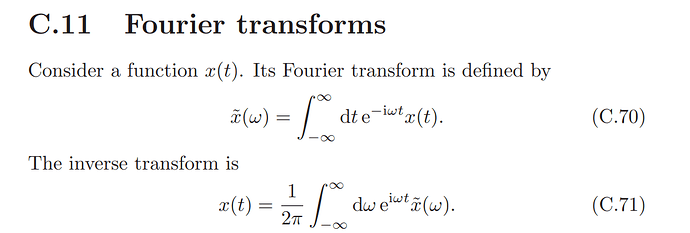Что из этого нужно знать, а что не обязательно? @Alisher @Ersultan
4 лайка
Эти интегралы встречаются часто, в олимпиадах их дают как подсказку?
1 лайк
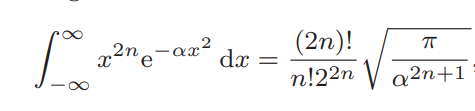
зета-функция Римана появляется при выводе формулы Планка о спектральной плотности излучении (а именно \xi(2)=\pi^2/6).
я вроде видел одну задачу с дельта-функцией, насколько я помню там было о напряжённости поля в пространстве при прохождении конечного заряда через прямой провод.
разложение в ряд фурье есть и в сивухине 3 том в главе с переменным током, там есть приложение об этой математике (ну и эта теория выражает, к примеру, то, что любой сигнал можно разложить на сумму гармонических сигналов)
полилогарифм вроде получается взятием производной из гамма-функции, но я не видел задач которые это применяют (как и формулу стирлинга)
якобиан хз
lagrange multipliers хз
а вот в конце интегралы появляются если из распределения максвелла рассчитать, например, \overline v, \overline{v^2}, \overline{v^3}, \overline{1/v} и т.д.
4 лайка
публика требует ссылок!
используется для перевода интегралов в другие единицы измерения (например из декартовых в полярные)
Для поиска минимумов и максимумов функций в 2Д и выше
4 лайка
Вроде множители лагранжа можно использовать в механике в уравнениях лагранжа первого рода для расчета силы реакции связей.
Я не думаю, что что-то из этого будет сильно полезно для олимпиад. На всякий случай стоит запомнить формулу стирлинга и нижние интегралы (может понадобиться на республиканских сборах, потому что там не дают математические подсказки)
7 лайков
Хорошо
1 лайк
Интересно, какая это книжка?
1 лайк
Blundell Thermodynamics
4 лайка
Статистическая физика и термодинамика обычно пользуются этим, но в олимпиадах по физике я не знаю, бывает это или нет.