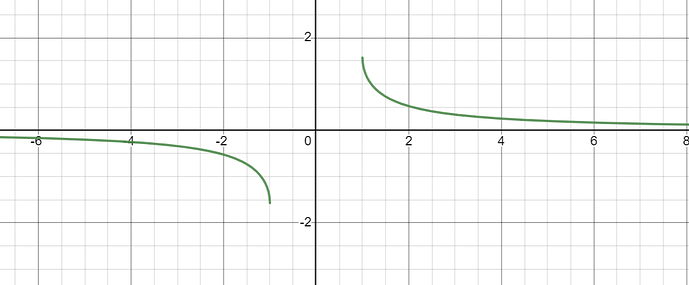
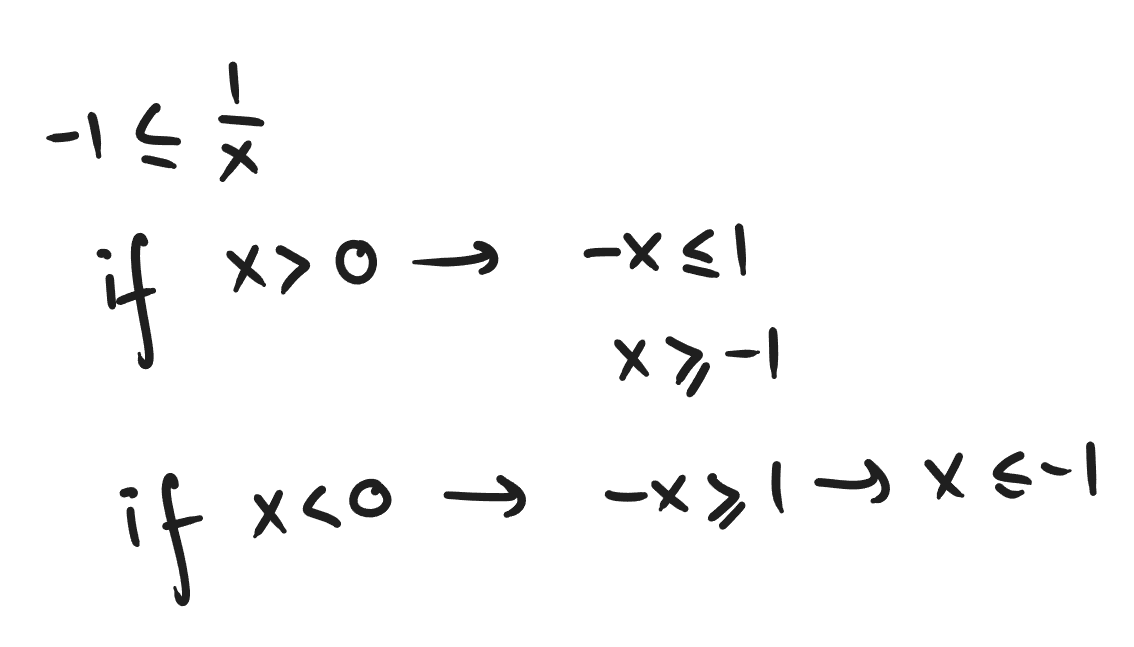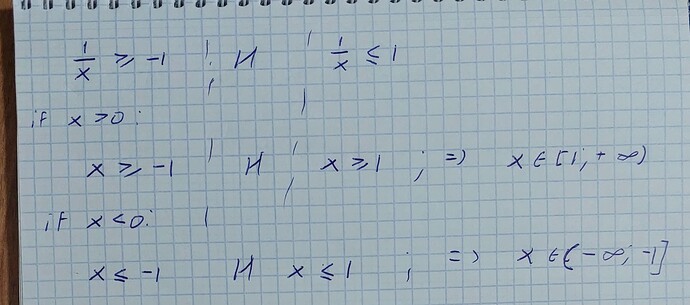Нужно найти область определения arcsin(\frac{1}{x}). Область определения арксинуса от -1 до 1 . Значит нужно решить неравенство -1 \leqslant \frac{1}{x} \leqslant 1 чтобы найти область определения для интересующей наш функции. Интуитивно я понимаю, что ответ (- \infty, -1) \bigcup (1, + \infty). Но решить неравенство не получается.
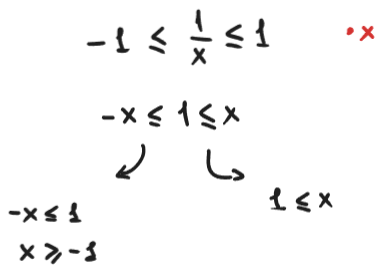
Я просто умножил всё на x и решил неравенства отдельно.
если знак больше или равно, тогда квадратные скобки же возле единиц . А так вроде у вас все правильно
ой да
почему? у меня вышло -1 \leqslant x . А должно выйти наоборот x \leqslant -1 . Может я неравенство неправильно построил? График функции:
а ой. Когда вы умножаете на отрицательное число, то знак неравенства меняется, поэтому рассмотрите отдельно случаи с x больше и меньше нуля, в первом же шаге, когда на него домножаете
1 лайк
тоже думал об этом. У меня выходит два ответа если взять только одно неравенство. Как теперь выбрать что правильнее?
Чтобы такой путаницы не было, удобнее еще записать неравенство с модулем
\frac{1}{|x|} \leq 1
2 лайка
а зачем выбирать? вот вы и получили ваш ответ, оба этих множества
Здесь для положительных x должны выполняться два условия:
x \geq -1
и из второго неравенства
x \geq 1
Тогда очевидно, учитывая, что при отрицательных значениях x \leq -1, x не может быть между -1 и 1
1 лайк
а как тогда объяснить расчетами, что x не принимает значения
Это же значит, что оно не может быть между 0 и -1? Мы же пришли к этим выводам, предполагая, что x>0. Поэтому с нуля до одного. Я правильно рассуждаю? А чтобы доказать, что x не может быть между -1 и 0, нужно рассмотреть когда x < 0. А вообще есть ли более быстрый метод вычисления? Рассматривать варианты значения x и сравнивать полученные ответы чет занимает много времени
ой хотел Амирбеку ответить.
Если x \leq 0, то ещё обязательно x \leq -1 (что вы и получили ранее из -1 \leq \frac{1}{x})
