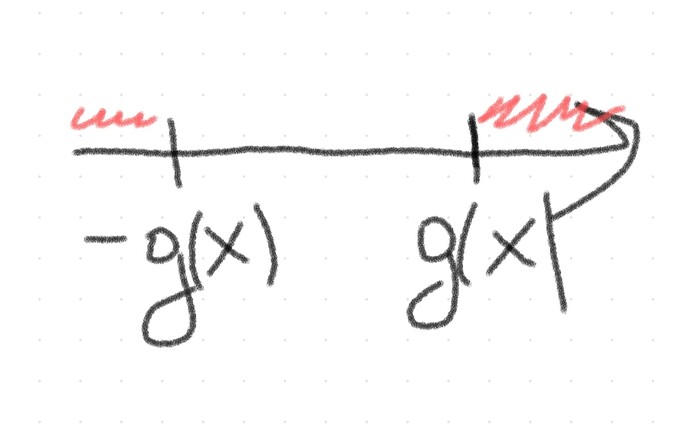Нигде не могу найти внятный ответ на то, почему в одном случае мы используем систему, а в другом совокупность. Был бы очень благодарен за объяснение.
Ну смотри, в первом ( левое неравенство) случае, у тебя значение значение f(x) по модулю не может быть по модулю больше, чем значение g(x). То есть значение f(x) должно лежать в промежутке от -g(x) до g(x) включительно. Это можно изобразить на графике( фото чуть ниже). Для данного случая можно взять любое значение для g(x), допустим у нас g(x)=2. Тогда при условии, что |f(x)|=< g(x) у нас f(x) может лежать в промежутке от -2 до 2. Система, так как f(x) не может выходить за эти рамки и с помощью двух уравнение ты, как будто задаешь рамки этого промежутка. Примером может послужить два значения для f(x).
f(x)=1=> лежит в промежутке от -2 до 2, так как оно выполняет условия обоих уравнений, поэтому данное значение входит в границы от -g(x) до g(x) и соответственно неравенство выполняется
f(x)=-50=> |f(x)| не лежит в промежутке от -2 до 2
Давай рассмотрим правое неравенство с модулем. |f(x)| больше либо равно g(x). Тогда f(x) наоборот не лежит в промежутке от -g(x) до g(x) не включительно. Тогда второе уравнение задает пространство на графике, которое меньше, чем -g(x), а первое задает значение пространство на графике, которое больше, чем g(x). То есть если рассмотреть в общем случае, то f(x) должно принимать значение от минус бесконечности до -g(x) включительно и от g(x) до + бесконечности включительно. Можно посмотреть рисунок ниже.
Рассмотрим пример. Если g(x) равно 5, то
f(x)=-10=> f(x) не лежит в промежутке от -5 до 5 и значение f(x) удовлетворяет неравенство
f(x)=3=> f(x) лежит в промежутке от -g(x) до g(x) и не равенство не удовлетворяется. Рисунок прикреплен ниже:
P.S:
можно сказать, в общем случае, что:
a) Если |f(x)| меньше или равно g(x), то оно лежит в промежутке от -g(x) до g(x) , то есть оно должно удовлетворять одновременно двум условиям( условия задающие границы)=> нужна система:
- f(x) больше, либо равно -g(x)
- f(x) меньше, либо равно g(x)
b) Если |f(x)| больше, либо равно g(x), то должно удовлетворяться лишь одно из условий=> нужна совокупность. Условия:
f(x) меньше, либо равно -g(x), либо f(x) больше, либо равно g(x)
Достаточно же построить желаемый интервал на графике и интервалы, получаемые от каждого из неравенств, не?