In this problem you should think of how the position of the center of mass of the system makes influence on dynamometer reading.
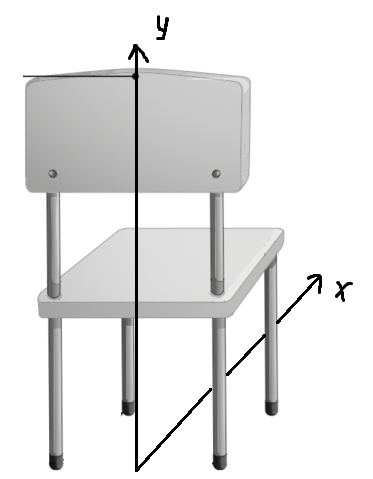
Consider the coordinate system shown above. The origin is on the intersection of the axis of symmetry with the line connecting the back legs of the chair. So the coordinates of center of mass are (x_C, y_C).
Then you write equations for the first two cases.
F_1 H=mg(a-x_C), \\
F_2H = mgx_C.
Considering the third case, it is understood that for minimum F_3 one should apply the force at a certain angle to the horizon.
Here are the equations for the third case.
F_3\cos\alpha H = (mg-F_3\sin\alpha)\frac{a}{2}.
Bearing in mind that mga = (F_1+F_2)H,
F_3(H\cos\alpha+\frac{a}{2}\sin\alpha) = \frac{F_1+F_2}{2} H,
and taking derivative \displaystyle\frac{dF_3}{d\alpha}=0, you may get \tan \alpha =\displaystyle\frac{a}{2H}, so the final answer is
F_3=(F_1+F_2)\displaystyle\frac{H}{\sqrt{a^2+4H^2}}=13.44\space\text{N}.
6 лайков
Amazing! Thank you.
1 лайк
