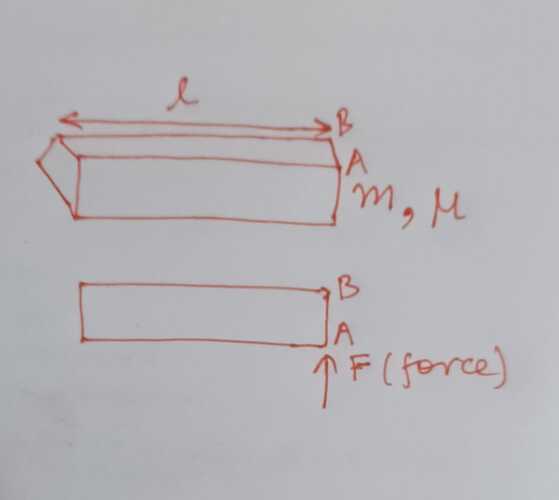
A cubical box of length l and mass M is placed on rough horizontal floor of coefficient of friction µ. The diagram is top view of box. If F is the minimum force by which the block starts rotating, find F. Please provide solution.
So, according to the condition of the problem, we see that this is a cubic box and it stands on some horizon and the force always has this direction.
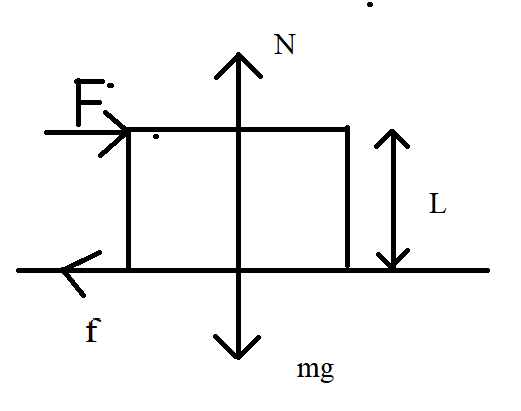
Yes this is the situation. We have to find minimum value of F to rotate the box. I have never done questions involving rotation of box on rough ground. These are different from toppling question, I think.
NOTE: The top view of the cubical box is shown in the question.
Ew, sorry. Ok, if put a small dot to left corner of the cube we can use the torque acting for in the clockwise direction [M_+=F*\frac{L}{2}+ f_{fric}*\frac{L}{2}] and in the anticlockwise direction [M_-=N*\frac{L}{2})]
The forse of friction:
f_{fric}=µmg
Then express the torque balance equation:
F = N-µmg=mg(1-µ)
This is only the first version of the solution that I made using all the data from the condition, but given that we have a minimum force, then the force and friction should equalize and the answer should come out like this:
F=mg/2
This is only the second version of the solution.
I don’t think that is the correct answer. We get this answer when we have to topple the cubical box. But the question is saying “rotate” the box.
hint: correct solution includes a little of integration
Please provide the correct solution. I have never encountered such problems before. The solution will make me understand better.
i’m not interfering here:) i’ll let Miras understand the solution on his own so he would explain
Oh, could you tell me the solution in private message, if it’s alright? I have got no idea how to solve. Otherwise, I and Miras will try more, I guess.
One problem I found online but this involves triangular lamina. Задача по физике - 13140 | Самые интересные факты о планете Земля. Новости науки и ответы на сложные вопросы. EarthZ.ru – всё о Земле!
Any progress, miras? I thought of taking a small element and then integrating but clearly that will not work here. The triangular lamina problem is different from this question.
Sorry for frivolity. So, in this task we have two points of application of friction forces and they have different torques.
By using the laws of dynamics, you can get the third equation:
After we integrate the first formula and equate the torques:
Could you tell why we have two different application of friction forces?