Задача 8. Положение точки на плоскости задаётся двумя числами — например, декартовыми координатами (x,y). Во многих случаях удобны полярные координаты (r,φ) точки M, где r есть расстояние от M до полюса — фиксированной точки O плоскости (то есть длина радиус-вектора r = OM), а φ — угол между радиус-вектором r и фиксированной осью (так называемой полярной осью). Запишите каноническое уравнение эллипса в полярных координатах, расположив полюс в центре симметрии эллипса и приняв ось x (рассмотренной выше системы координат) в качестве полярной оси.
Что тут я могу поделать, можете показать рисунком что за угол φ а то не совсем понял, что за полярная ось
1 лайк
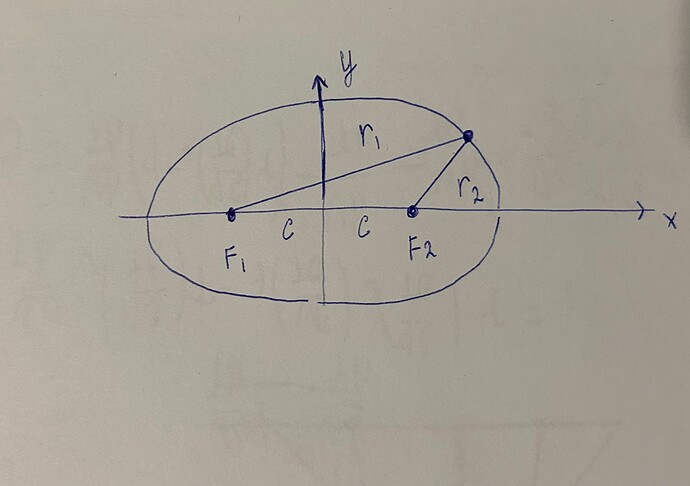
В общем здесь нужно выбрать какую-то точку на эллипсе и с обоих фокусов F_1, F_2 провести радиус векторы r_1,r_2.
Ты можешь полярный угол \varphi взять как угол между r_1 и горизонтальной осью. Дальше r_1 можно заменить r и r_2 можно выразить через r и угол \varphi с помощью теоремы косинусов. Также учитывай то, что c=ea, где e-эксцентриситет эллипса
5 лайков
Ответ через a и b , думаю сразу написать a^2-b^2=c^2 рахмет вам большой
1 лайк