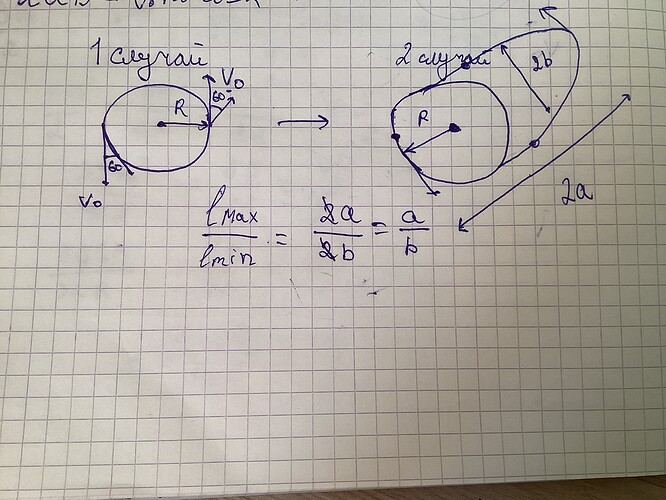
Два одинаковых тела вращаются по круговой орбите вокруг общего центра масс под действием сил гравитационного притяжения. В некоторый момент времени векторы скоростей тел мгновенно поворачиваются в плоскости орбит в разные стороны на один и тот же угол а = 30° без изменения своих абсолютных значений (рис. 132). Найти отношение максимального и минимального расстояний Imax/lmin между телами при их дальнейшем свободном движении.
Хотел спросить правильно ли я иду. На рисунке я хотел показать что когда спутнике отклонялись они начнут по эллипсу двигаться. И их максимальные расстояние это большая полуось а минимальное расстояние это малая полуось.
Правильно ли я мыслю ?
Да.
Рисунок ко второму случаю немного некорректный. Он был бы верно нарисован, если бы спутники увеличивали скорость только по модулю. Движение спутника идёт по такому эллипсу, что софокусен изначальной круговой траектории, а его большая ось всё так же равна 2R (это очевидно по той причине, что механическая энергия спутника после поворота не изменилась). Изучи побольше про геометрию эллипса и таким образом найди малую ось.
Я вас понял но все таки уточню. Вы имеете виду что, они будут двигаться по эллипсу где большая полуось равно 2R а малую полуось надо найти?
Мм… а почему нельзя тогда просто решить задачи таким образом ?
b=(R*r)^1/2
2a=r+R
R апогей; r перигей
Можно) Вопрос был касательно того, умеешь ли ты выводить с нуля эту формулу.
Эту формулу я кстати не знаю как выводиться
Можешь начать отсюда; в Википедии есть много формул и рисунков по геометрии конических сечений.