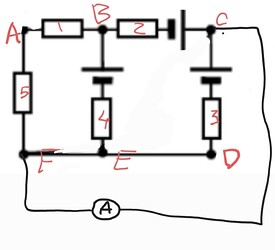
Главный плюс идеального вольтметра (вольтметр с бесконечно большим сопротивлением) в цепи в том, что он создаёт участок цепи, на котором ток не идёт. Поэтому мы просто можем его стереть, не влияя на результат.
Амперметр, напротив, создаёт участок цепи с нулевым сопротивлением. Участки FE и DE соединены проводами, у которых тоже нулевое сопротивление (это справедливо для всех задач с цепями, если не написано обратного). При любом токе, на участке с нулевым сопротивлением, напряжение будет равно нулю (U = IR, R =0 => U = I•0 = 0). Обычно, в задачах это используется чтобы соединить точки, но на данном этапе это только усложнит задачу, поэтому нам это не нужно, потому что, это только усложнит задачу. Лучше будет немного перерисовать схему чтобы контуры можно было легко определить.
Далее остаётся записать и решить уравнения Кирхгофа для контуров. Чтобы оставить возможность самому записать уравнения, я скрою их в качестве спойлера.
Для контура EBAF
\varepsilon = I_4R + I_1 + I_5
(I_1 = I_5)
Контур BCDE
Если мы возьмём маленький контур BCDE, то у нас будет маленькое уравнение, но ЭДС будет мешаться делая уравнение сложным для работы, ведь нам нужно найти ток:
\varepsilon = I_4R + I_2R – I_3R
Контур ABCDEF
А вот если взять больший контур ABCDEF, в котором 2 ЭДС, которые сокращаются, то получится очень удобное уравнение, с точками и сопротивлениями, где сопротивления сокращаются:
0 = I_2R – I_3R – I_5R – I _1R\\
I_2 = I_3 + I_5 + I_1
Самый большой контур
Остаётся самый большой контур с амперметром, для которого записываем простое уравнение:
\varepsilon = I_2R – I_1R – I_5R
У нас есть уже 3 уравнения, но неизвестных 6, поэтому нужно записать недостающие уравнения для узлов по 1 закону Кирхгофа
Узел В:
Узел С:
И как мы помним, F, E, D в одну точку, так как между ними разность напряжений равна нулю.
Решая эти уравнения, можно прийти к решению задачи. Так как ответ есть под условием, решение уравнений оставляется читателю в качестве индивидуального задания.
Осталось только найти напряжение на вольтметре по контуру ABCD-вольтметр:
0 = I_1R+ I_3 R – I_2R – V
Если возникли неправильные знаки, значит, ток идёт в обратную сторону или разность потенциалов уменьшается в обратную сторону. Не стоит беспокоится, это частое явление в задачах со сложными схемами. Так как это приборы, то в ответе достаточно привести значение по модулю