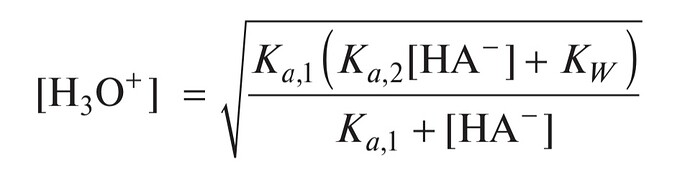Помогите вывести pH через константы и C_{0} для раствора гидро- или дигидрофосфата натрия. Хотел вывести как для H3PO4, но ответ не сходится как в учебнике. Пробовал написать Na+ в ур. электронейтральности, не помогло. Не хочется просто запомнить и использовать эту формулу:
1 симпатия
А покажи свой ответ, может у тебя просто более точно получилось
2 симпатии
Upd: в последнем выражении, в знаменателе, в последнем слагаемом не должно быть [H+]
1 симпатия
Задача: Рассчитайте рН водного раствора с 0,0100 М концентрацией растворенного вещества: а) фосфорной кислоты; б) дигидрофосфата натрия; в) гидрофосфата натрия; г) тринатрийфосфата. Ответ: а) рН 2,26; б) рН 4,79; в) рН 9,52; г) рН 11,86.
С моим выражением выходит pH = 12.30
Ну, смотри, ты же прикидываешь на глаз, что у тебя pH гидрофосфата будет что-то среднее между pK_{a,2} и pK_{a,3}. Это просто следует из диаграммы форм.
А раз так, то ты можешь либо прям сразу в в своём первом выражении для электронейтральности или уже после всех преобразований, прикинуть порядок каждого члена выражения и выкинуть супермелкие.
Т.к. у тебя [\ce{H+}] \approx 10^{-10} -10^{-9}, то легко можно заметить, что [\ce{H+}]^3 \approx 10^{-30}-10^{-27}, а соседнее с ним слагаемое K_1K_2[\ce{H+}] \approx 10^{-19} -10^{-18} и получается можно выкинуть спокойно куб концентраций протонов из уравнения. А вот K_1[\ce{H+}]^2 \approx 10^{-20} -10^{-22} и такое уже выкинуть нельзя, слишком близки значения
Должно получиться в итоге, когда от всего лишнего избавишься
2С_{соли}^0=С_{соли}^0\cdot
\frac{[\ce{H+}]^2K^a_1+2[\ce{H+}]K^a_1K^a_2+3K^a_1K^a_2K^a_3}
{[\ce{H+}]^2K^a_1+[\ce{H+}]K^a_1K^a_2+K^a_1K^a_2K^a_3}+K^w/[\ce{H+}]
или
2С_{соли}^0=С_{соли}^0\cdot
\frac{[\ce{H+}]^2+2[\ce{H+}]K^a_2+3K^a_2K^a_3}
{[\ce{H+}]^2+[\ce{H+}]K^a_2+K^a_2K^a_3}+K^w/[\ce{H+}]
Если выкинешь тут гидроксид, выйдет у тебя формула типичная для амфолитов pH=(pK_2+pK_3)/2=9.94
Оставишь всё как есть, получишь кубическое, но практически точный ответ 9.56
C[\ce{H+}]^3-[\ce{H+}]^2K^w-(CK_2K_3+K_2K^w)[\ce{H+}]-K^wK_2K_3=0
В самом кубическом можно еще что-то в принципе убрать (свободный член и квадратный, они мелкие), но немного пострадает тогда точность, капельку совсем
C[\ce{H+}]^3-(CK_2K_3+K_2K^w)[\ce{H+}]=0 \\
\left[ \ce{H+} \right]=\sqrt{\frac{CK_2K_3+K_2K^w}{C}}
3 симпатии
Сперва напишем все возможные процессы:
Na_2HPO_4 \to 2 Na^+ + HPO_4^{2-}
HPO_4^{-2} + H_2O \to H_2PO_4^{-} + OH^- ka_2
HPO_4^{-2} + H_2O \to PO_4^{-3} + H_3O^+ ka_3
H_2PO_4^{-} + H_2O \to H_3PO_4 + OH^- ka_1
H_2O + H_2O \to H_3O^{+} + OH^- k_w
Теперь напишем уравнение электроотрицательности:
\sum (+) = \sum (-)
[Na^+] + [H_3O^+] = 2 [HPO4^{-2}] + [H_2PO4^-] + 3 [PO_4^{-3}] + [OH^-]
И теперь мат. баланс:
C_0 = [HPO4^{-2}] + [H_2PO4^-] + [PO_4^{-3}] + [H_3PO_4]
примечание: C_0 это конц. c[Na_2HPO_4]_{начальное}
Сперва выразим концентрацию гидрофосфата через мат. баланс:
C_0 - [H_2PO4^-] - [PO_4^{-3}] - [H_3PO_4] = [HPO4^{-2}]
теперь подставляем под уравнение электронейтральности:
2 \cdot C_0 = [Na^+]
2 \cdot C_0 + [H_3O^+] = 2 \cdot (C_0 - [H_2PO4^-] - [PO_4^{-3}] - [H_3PO_4]) + [H_2PO4^-] + 3 [PO_4^{-3}] + [OH^-]
раскрываем скобки и сокращаем что можно и следующий вид уравнение:
[H_3O^+] = [PO_4^{-3}] + [OH^-] - 2 [H_3PO_4] - [H_2PO4^-]
или так:
[H_3O^+] + 2 [H_3PO_4] + [H_2PO4^-] = [PO_4^{-3}] + [OH^-]
начинаем выражать конц. через константы:
[H_2PO4^-] = \frac{{[HPO_4^{-2}]}{[H^+]}}{ka_2}
[PO_4^{-3}] = \frac{{ka_3}{[HPO_4^{-2}]}}{[H^+]}
[H_3PO4] = \frac{{[H2PO_4^{-}]}{[H^+]}}{ka_1} \longrightarrow \frac{{[HPO_4^{-2}]}{[H^+]^2}}{{ka_2}{ka_1}}
скажем так что H_3PO4 очень малое количество образуется и будем пренебрегать этой стадией:
[H_3O^+] + [H_2PO4^-] = [PO_4^{-3}] + [OH^-]
[H^+] + \frac{{[HPO_4^{-2}]}{[H^+]}}{ka_2} = \frac{{ka_3}{[HPO_4^{-2}]}}{[H^+]} + \frac{k_w}{[H^+]}
дальше решаем это уравнение:
\frac{{ka_2[H^+]}+{[HPO_4^{-2}]}{[H^+]}}{{{ka_2}}} = \frac{{ka_3}{[HPO_4^{-2}]}+{k_w}}{[H^+]}
дальше делаем преобразование:
[H^+]^2 = \frac{({ka_3}{[HPO_4^{-2}]}+{k_w}){ka_2}}{{ka_2}+{[HPO_4^{-2}]}}
или же:
[H^+] = \sqrt\frac{({ka_3}{[HPO_4^{-2}]}+{k_w}){ka_2}}{{ka_2}+{[HPO_4^{-2}]}}
7 симпатий
на будущее, чтобы уравнения не были такими кучными, можно выделять их в блоки, если знаки доллара ставить на отдельной строке. Например e^{-\frac{E_A}{RT}} $e^{-\frac{E_A}{RT}}$
Или:
e^{-\frac{E_A}{RT}}
$$
e^{-\frac{E_A}{RT}}
$$
P.S. Я было хотел поправить ваши реакции, но зачем вы каждую формулу обделяли отдельным долларом??