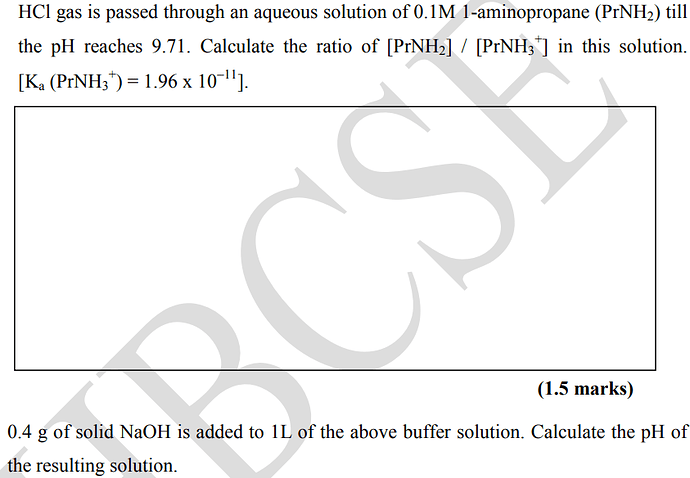Вышли затруднения при решении второго пункта этой задачи. Через данные из пункта 2 вытащил концентрации двух форм амина (прот: 0.00913 , депрот: 0.09087) в буферном растворе до добавления щелочи. После добавления весь протонированный амин переходит в депрот. и остается 8.7*10^-4 М щелочи. После устанавливается равновесие и тут я посчитал через квадратное уравнение равновесные концентрации раствора и через него основность. В конечном итоге у меня вышла кислотность=11.88, а в ответе 10.08. Пожалуйста помогите и укажите на ошибку
Ты попутал может формы. У меня наоборот, протонированной в первом случае больше. А вообще, тебе не нужно для второго пункта первый. Ты просто в электронейтральности уравнении не забываешь про концентрацию хлорида и всё должно сойтись красиво.
Согласен с @Sammael Реакция:
\ce{PrNH2}+\ce{H2O}\rightarrow \ce{PrNH3^+}+\ce{OH^-}
У нас раствор основания возьмём основания как B:
\ce{K_\ce{b}}=\frac{[\ce{BH^+}][\ce{OH^-}]}{[\ce{B}]}
Уравнение для буфера:
\ce{pOH}=\ce{pK_\ce{b}}+\log\frac{[\ce{BH^+}]}{[\ce{B}]}\\
4.29=3.29+\log\frac{[\ce{BH^+}]}{[\ce{B}]}\\
10=\frac{[\ce{BH^+}]}{[\ce{B}]}
По материальному балансу находим концентрации веществ:
c_B=[\ce{B}]+[\ce{BH^+}]=11[\ce{B}]=0.1\\
[\ce{B}]=9.1\cdot 10^{-3}\ce{M}\\
[\ce{BH^+}]=0.091\ce{M}
Во втором пункте добавляют щёлочь с концентрацией (0.4/40)/1=0.01 моль/л. Гидроксид ионы реагируют с пропиламином:
\ce{PrNH3^+}+\ce{OH^-}\rightarrow \ce{PrNH2}+\ce{H2O}
Концентрация оставшегося протонированного ионы 0.091-0.01=0.081 моль/л , в ходе реакции образуется и пропиламин концентрацей 0.0191. Находим pOH:
\ce{pOH}=3.3+\frac{0.081}{0.0191}=3.92
pH=14-pOH=14-3.92=10.08
4 лайка
Спасибо, глупая ошибка, при вычислении молярностей
Стоит отметить, что в таких задачах порой бывает очень опасно не учитывать константу равновесия нейтрализации. Как ты и сказал, протекает реакция:
BH^{+} + OH^{-} = B + H_{2}O
Константа равновесия этой реакции составляет \frac{K_{a}}{K_{w}} = 1960 (потому что -RTlnK_{reaction} = -RTlnK_{a} - (-RTlnK_{w}) ). И как можно заметить, значение константы заставляет остановиться и немного подвергнуть сомнению то, что можно считать, что OH^{-} полностью прореагирует. В действительности, если так посчитать, то ответ в принципе не изменится:
K_{reaction} = \frac{9.1 \cdot 10^{-3}+x}{(0.091-x)(0.01-x)} = 1960
Отсюда x = 9.8806 \cdot 10^{-3} M , и [OH^{-}] = 1.194 \cdot 10^{-4} M, значит pH = 14 + log_{10}(1.194 \cdot10^{-4})= 10.08
К чему я веду ? К тому, что всегда надо проверять, можно ли делать такое пренебрежение, или нет. Я сам часто встречался с тем, что казалось бы, протекает реакция нейтрализации в буферном растворе, однако там равновесие далеко не сильно смещено в сторону продуктов, и приходится так углубляться в детали
2 лайка