Подсказки:
- второй закон ньютона
- \theta - искомый угол, можно найти через отношение ускорений
Решение
ma=mg\sin\alpha-\mu mg\cos\alpha \\
a=g\sin\alpha-\mu g\cos\alpha
Получили ускорение сосуда, направленное вдоль наклонной плоскости.
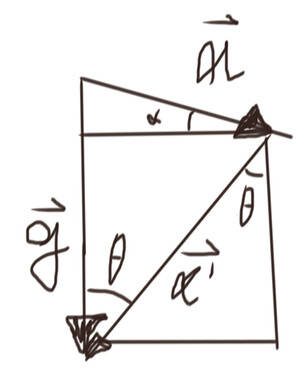
Рассмотрим теперь ускорения. В общем, схема будет выглядеть как-то так (рисунок к задаче, часто может значительно упростить решение):
Тогда по определению
\sin \theta = \frac{a}{g} = \sin \alpha - \mu \cos \alpha
Отсюда уже можно выражать \theta
P.S. как я заметил в другой теме, Алишер уже предлагал решать 1001. Я точно помнб, что в ней была такая же или очень похожая задача. Савченко, как мне говорили - это уже хорошая подготовка конкретно перед областью в 9, 8 классе
1 лайк
вектора указал правильно, но у тебя ошибочка в выкладках
2 лайка
Там нет такой задачки я уже прочалил гидростатику в 1001,там по идее не в тему гидростатика,одни вопросы какие то,а не задачи
1 лайк
может вы имели ввиду похожую задачу на импульс?там тоже сосуд с одой спускался по склону просто она еще выходила
Спасибо за решение,я что то его не срезу заметил)
1 лайк
ой а где
возможно, в механике что-то такое было
подумай
1 лайк
Ещё не хватает этого?
a = g\tan \theta \\
мимо(
правильно вырази \tan\theta через твой рисунок
3 лайка
Так?
\tan \theta = \frac{a\cos \alpha}{g-a\sin\alpha}
ну вот) раскрывай и добивай до конечного ответа
p.s.
\tan{(\alpha-\beta})=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}
2 лайка
\tan \theta = \frac{g\cos\alpha(\sin\alpha-\mu\cos\alpha)}{g(1-(\sin\alpha-\mu\cos\alpha)\sin\alpha)} \\
\tan \theta = \frac{\tan\alpha - \mu}{\tan^{2}\alpha - \mu\tan\alpha-1-\tan^{2}\alpha} \\
\tan \theta = \frac{\mu-\tan\alpha}{\mu\tan\alpha+1}
5 лайков
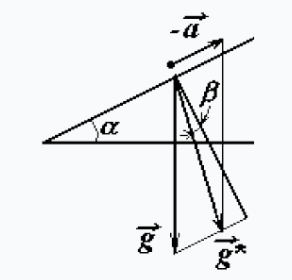
Ускорение сосуда, скользящего по наклонной плоскости, определяется формулой
a = g ( \sin \alpha - \mu \cos \alpha)
и направлено вдоль наклонной плоскости.
Рассмотрим воду в системе отсчета, связанной с сосудом. Естественно, эта система неинерциальная. Можно ввести эффективное ускорение свободного падения \vec{g}^{*} = \vec{g} - \vec{a}. Поверхность воды перпендикулярна вектору \vec{g}^{*} (так как в этой системе вода покоится). Из рисунка следует, что искомый угол \beta определяется
\tan \beta = \frac{g \sin \alpha - a}{ g \cos \alpha} = \mu
Относительно горизонта, угол будет составлять
\boxed{\delta = α − \arctan \mu}
Источник: savchenko-physics.github.io
4 лайка