Савченко Электрические цепи Аттенюатор

[Damir_K (-6)]

Аттенюатор представляет собой делитель напряжения, схема которого представлена на рисунке. Каковы должны быть сопротивления R1 и R2, чтобы на каждом следующем сопротивлении R1 напряжение было в десять раз меньше, чем на предыдущем?

Пытался решить но не могу найти второе уравнение:Рассмотрел последнею ячейку и вышло

Дальше не знаю как решить, ответ в задачнике:R1=9r

[Argyn (Argyn Seitkamit)]

Рассмотри еще одну ячейку, которая идет до. Потом делаешь все точно так же, и получаешь систему из 2 уравнений с двумя неизвестными R_1 и R_2

[Damir_K (-6)]

я так тоже пытался кажется в математике ошибся

[Sulta_nnn (Sula🛌)]

можете пожалуйста объяснить как вы взяли последнюю ячейку?

[misqwx (misqwwx)]

надеюсь понятно выглядит, если нет то напиши я нормально распишу

[astrosander1 (Aliaksandr Melnichenka)]

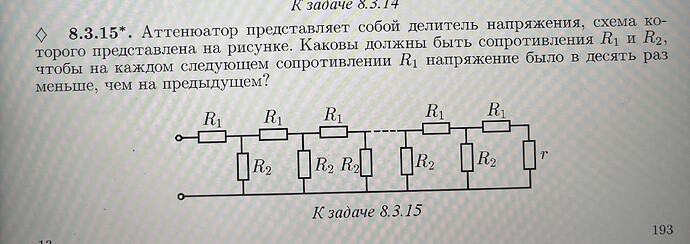
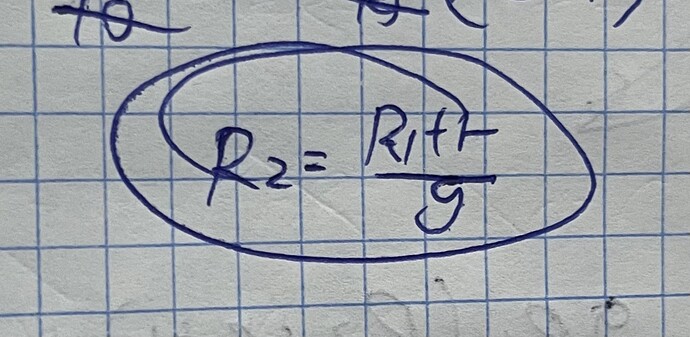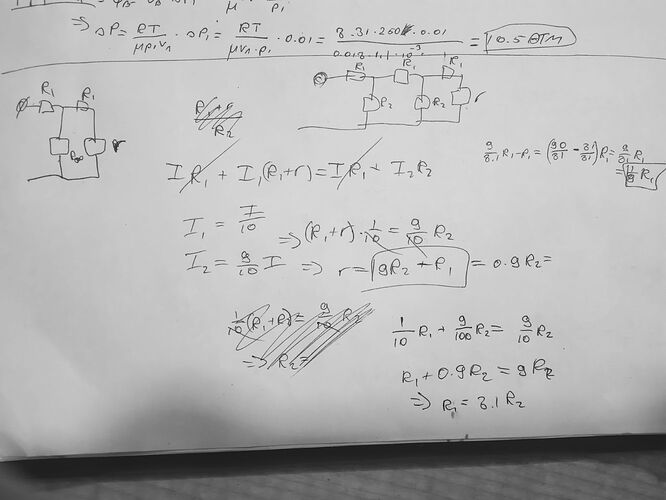Рассмотрим следующий рисунок.

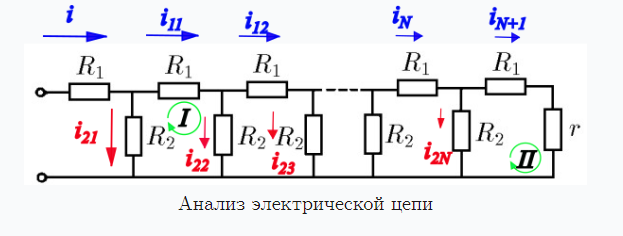
Применение второго закона Кирхгофа. Для контура I

-i_{11}R_1-i_{22}R_2+i_{21}R_2=0

-i_{11}R_1+R_2(i_{21}-i_{22})=0 \;(1)

Так как i_{11}R_1 = 10 i_{12}R_1, то есть, i_{1n} = 10 i_{1(n+1)}, следовательно

i_{1n} = \frac{i_{11}}{10^{n-1}} \;\forall~n\geq2 \;(2)

Для контура II и согласно (2)

-i_{N+1}(R_1+r)+i_{2N}R_2=0

-\frac{i_{11}}{10^{N-1}}(R_1+r)+i_{2N}R_2=0 \;(3)

Для последующих бифуркаций (с применением первого закона Кирхгофа)

i_{11} = i_{12}+i_{22}

i_{22} = i_{11}-i_{12}

Таким образом,

i_{2n} = i_{1(n-1)}-i_{1n} \;\forall~n\geq2 \;(4)

Согласно (2), изменим (4)

i_{2n} = \frac{i_{11}}{10^{n-2}}-\frac{i_{11}}{10^{n-1}}

i_{2n} = \frac{9i_{11}}{10^{n-1}} \;(5)

Подставим (5) в (3)

9R_2 = R_1+r \;(6)

Подставим (5) в (1)

R_1 = \frac{81}{10} R_2 \;(7)

Наконец, решая систему уравнений, образованную (6) и (7), получаем

\boxed{R_1 = 9r}

\boxed{R_2 = \frac{10}{9}r}

Источник: savchenko-physics.github.io