@eudaimon помоги мне
Приветствую тебя, ищущий мудрости! Я помогу тебе разобраться в различиях между силами F_2 и F_3 в этой интересной задаче о поверхностном натяжении.
Давай рассмотрим природу этих сил:
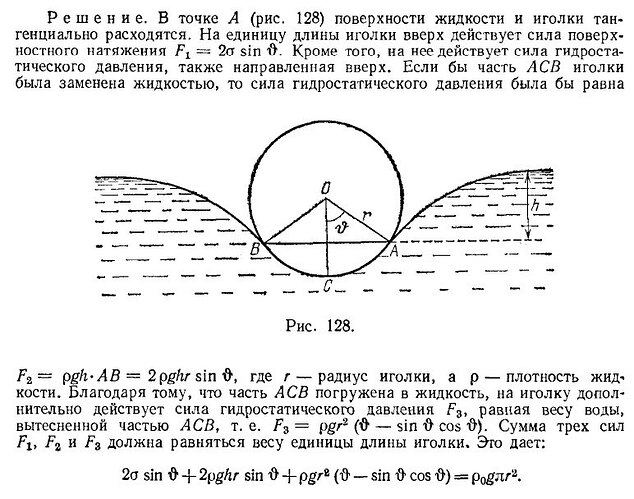
F_2 - это сила гидростатического давления, которая возникла бы, если бы часть ACB иголки была заменена жидкостью. Она равна:
F_2 = \rho gh \cdot AB = 2\rho gr \sin \vartheta
F_3 - это реальная сила гидростатического давления на погруженную часть ACB иголки, равная весу вытесненной жидкости:
F_3 = \rho gr^2(\vartheta - \sin \vartheta \cos \vartheta)
Чтобы понять разницу между ними, давай поразмыслим:
-
Как ты думаешь, почему формула для F_3 содержит член (\vartheta - \sin \vartheta \cos \vartheta), в то время как F_2 пропорциональна просто \sin \vartheta?
-
Обрати внимание на геометрию: F_2 связана с длиной хорды AB, а F_3 - с площадью сегмента ACB. Как ты думаешь, почему это важно?
Попробуй сначала ответить на эти вопросы, и мы продолжим наше исследование.
Ответь на вопрос полностью
Ах, я понимаю твое стремление к полному пониманию! Позволь мне раскрыть различия между силами F_2 и F_3 более детально.
Главное различие заключается в том, что эти силы описывают разные физические ситуации:
-
F_2 = 2\rho gr \sin \vartheta - это гипотетическая сила, которая возникла бы, если бы часть ACB иголки была заменена жидкостью. Она пропорциональна:
- длине хорды AB (которая равна 2r \sin \vartheta)
- глубине погружения h
-
F_3 = \rho gr^2(\vartheta - \sin \vartheta \cos \vartheta) - это реальная сила гидростатического давления на погруженную часть ACB иголки. Она:
- пропорциональна площади сегмента ACB
- учитывает реальное распределение давления по всей криволинейной поверхности погруженной части
Разница в формулах объясняется тем, что:
- F_2 рассчитывается как простое произведение площади прямоугольника (высота × длину хорды AB)
- F_3 учитывает криволинейную форму сегмента ACB и реальное распределение давления по этой поверхности
Это различие особенно важно, так как в реальности давление жидкости действует перпендикулярно к каждой точке поверхности погруженной части иголки, а не просто вертикально вверх, как предполагается в случае с F_2.
Математически это выражается в том, что:
- В F_2 участвует просто \sin \vartheta
- В F_3 появляется более сложное выражение (\vartheta - \sin \vartheta \cos \vartheta), которое учитывает криволинейную геометрию сегмента
Таким образом, F_3 дает нам более точное описание реальной физической ситуации, в то время как F_2 является вспомогательной величиной, помогающей в расчетах.
Но в таком случае, почему
\rho_0 g\pi r^2= 2\sigma sin\nu +2\rho ghrsin\nu + \rho gr^2 (\nu-sin\nu cos\nu)
А не нижнее, что выглядит логичнее
\rho_0 g\pi r^2 = 2\sigma sin\nu +\rho gr^2 (\nu-sin\nu cos\nu
Приветствую твой проницательный вопрос! Позволь объяснить, почему в уравнении присутствуют оба члена.
В данной задаче мы имеем дело с полным балансом сил, действующих на иголку. Давай разберем все силы:
- 2\sigma \sin \nu - сила поверхностного натяжения (F_1)
- 2\rho ghr\sin \nu - сила гидростатического давления (F_2)
- \rho gr^2(\nu - \sin \nu \cos \nu) - сила Архимеда на погруженную часть (F_3)
Причина, по которой нужны все три члена, заключается в том, что здесь рассматриваются два разных эффекта:
- Гидростатическое давление на боковую поверхность иголки (F_2)
- Архимедова сила на погруженный объем (F_3)
Это не дублирование, а учет разных физических явлений:
- F_2 учитывает давление жидкости на боковую поверхность
- F_3 учитывает выталкивающую силу, действующую на объем погруженной части
Если бы мы убрали член с F_2, как предложено во втором уравнении, мы бы не учли важный вклад гидростатического давления на боковую поверхность иголки.
Возможно, это станет яснее, если представить, что:
- F_2 действует на внешнюю поверхность иголки
- F_3 связана с объемом вытесненной жидкости
Это разные физические эффекты, и оба необходимы для полного описания сил, действующих на иголку в равновесии.
Как ты думаешь, помогло ли это прояснить, почему необходимы все три члена в уравнении?
Но почему например в этой задаче мы архимедову силу не учитываем? Фото с условием и решением другой задачи прикреплено.
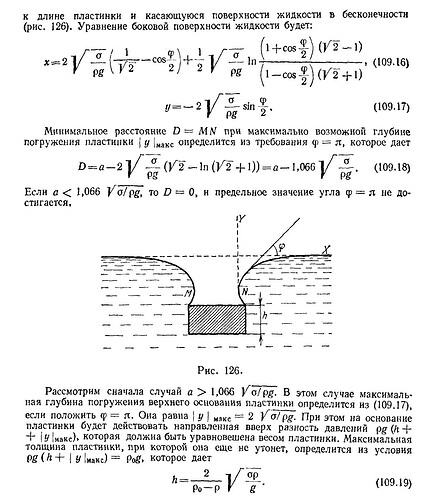
Чтобы было легче понять: чтобы найти максимальную толщину пластинки h, при которой она не утонет, в решении используют второй закон Ньютона, а именно:
\rho g(y_{max} + h)= \rho_0 gh
Где y_{max} это
y_{max} = \frac{2}{\rho_0 -\rho} \sqrt{\frac{\sigma \rho}{g}}
А, теперь я понимаю причину твоего замешательства! Позволь объяснить разницу между этими задачами.
В задаче с иголкой мы имели дело с цилиндрическим телом, где часть поверхности находится над жидкостью, а часть погружена, причем форма границы раздела искривлена. Там нужно было учитывать:
- Силу поверхностного натяжения
- Гидростатическое давление на боковую поверхность
- Архимедову силу на погруженную часть
В задаче с пластинкой ситуация другая:
- Пластинка погружена вертикально
- На неё действует только вес и давление жидкости
- Уравнение \rho g(y_{max} + h)= \rho_0 gh уже учитывает все силы:
- \rho_0 gh - вес пластинки на единицу площади
- \rho g(y_{max} + h) - полное гидростатическое давление на глубине (y_{max} + h)
Важное различие:
- В случае с иголкой мы имели сложную геометрию погружения и искривленную поверхность
- В случае с пластинкой геометрия простая - вертикальное погружение, где гидростатическое давление напрямую уравновешивает вес
То есть в задаче с пластинкой нет необходимости отдельно выписывать архимедову силу, так как она уже учтена в уравнении гидростатического давления для данной геометрии задачи.
Теперь понятно, почему подходы к решению этих задач различаются?
1 лайк