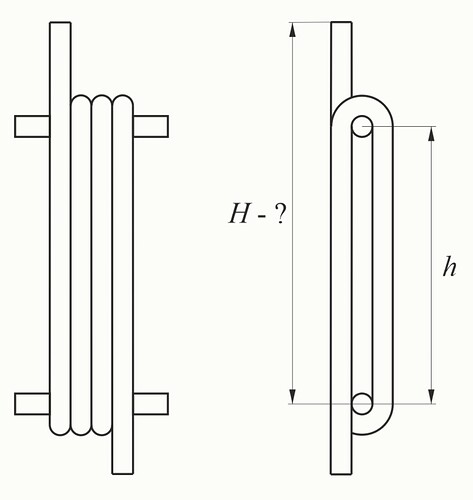
Гибкий шланг намотан на два горизонтальных стержня, расположенных один под другим на расстоянии h=0,5 м. Шланг делает вокруг стержней три полных оборота. Диаметры шланга и стержней малы по сравнению с h. В уходящий наверх конец шланга начинают наливать воду.
а)До какой высоты H поднимется вода в этой части шланга, прежде чем начнет выливаться с другого конца? (в метрах).
б) Если расстояние h увеличить в 10 раз, то высота H увеличится не в той же пропорции. Почему?
в) Найдите высоту H (в метрах) для h=5 м. Плотность воды ρ≈1000 кг/м3, атмосферное давление p0≈105 Па.
Основная идея этой задачи состоит в том, что нужно учесть образование воздушного пространства внутри шланга.
Пронумеруем вертикальные сегменты шланга от 0 до 6, где в нулевой сегмент наливают воду, а из шестого она выливается.
Подробнее о самом процессе наполнения воды. На рисунке внизу слева вода набирается поровну в нулевую и первую части. Когда же её высота достигает h, то она начинает перетекать из первого колена, набирая одновременно второе и третье колена (на рисунке справа показано сечение колен 1-2, а чёрным штрихом указан переход к третьему сегменту).
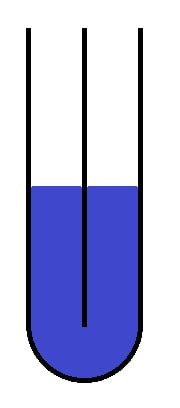

Таким образом появится воздушная полость в сегменте шланга номер 2. Аналогично происходит и с четвёртым коленом. Если обозначить толщину полости в номере 2 через \Delta_1, а в номере 4 – \Delta_2, то в конечном итоге вода заполняет каждое колено по-разному, высоты этих столбов такие:
0 - H
1 - h
2 - h-\Delta_1
3 - h
4 - h-\Delta_2
5 - h
6 - слив воды.
Далее, с учётом того, что давление воздуха в полости \Delta_1 равен p_1, а в \Delta_2 равен p_2, то применим закон Бойля-Мариотта pV=const и запишем равенство давления во всех точках шланга (давление снаружи равно атмосферному p_0):
Получилась система из пяти уравнений с пятью неизвестными. Чтобы её решить, выразим Δ_2 в последнем уравнении и решим соответствующее квадратное уравнение
Знак перед дискриминантом я взял положительный, так как отрицательная высота не имеет физического смысла. Соответственно выразим \Delta_1
Эти выражения довольно громоздки, и будет несколько затруднительно дать конечный ответ для H. Численные значения для h=0.5 \space м: \Delta_2 = 0.477 \space м, \Delta_1 = 0.457 \space м. Для h=5 \space м: \Delta_2 = 3.660 \space м, \Delta_1 = 3.001 \space м.
Получим окончательное выражение для H:
При h=0.5 \space м будет H = 1.43 \space м, при h=5 \space м получается H = 11.66 \space м.
Для протокола: мы решили оставить задачу поскольку она была довольно интересной. При этом, мы сразу узнали, что задача была частью турнира Ломоносова. Именно поэтому мы ответили после окончания олимпиады.
Мы рады помогать в изучении физики, но форум спроси никогда не будет механизмом нарушения академической честности на олимпиадах. Это так, заметка на будущее.