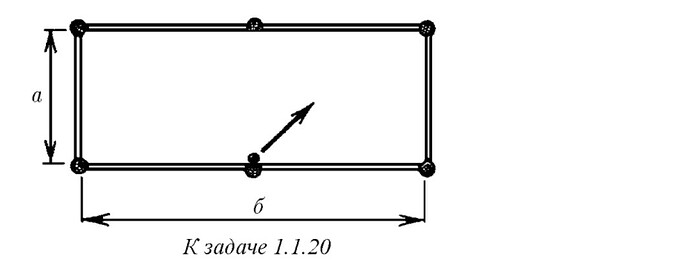
По биллиардному столу со сторонами а и б пускают шар от середины стороны б. Под каким углом к борту стола должен начать двигаться шар, чтобы вернуться в ту же точку, из которой он начал свое движение?
Можете помочь с этой задачей?Какое условие должно выполняться для этого могли бы вы подсказать?
https://youtu.be/POHquEKN3wE?si=9dqTttgIM9j0Pqy7 тут подробно решено. Но оно не в русском языке
2 лайка
Я видел это видео но не могу понять решение можешь объяснить почему он отметил на плоскости эти точки?
На майл ру есть решение. Там вроде нормально так обесьнили
http://otvet.mail.ru/question/65296254/
2 лайка
Можешь глянуть это видео про аналогичную задачу, там хорошо рассказано про
этот метод.
4 лайка
Можно решить проще, без заморочек с отражением. Движение можно разделить по двум осям. Ось Х вдоль длинной стороны стола. Ось У вдоль короткой стороны. Столкновения которые меняют скорости вдоль одной оси, никак не влияют на другую. Модуль скоростей по осям не меняется
Чтобы шар вернулся в ту же точку должны выполнятся определённые условия по обеим осям.
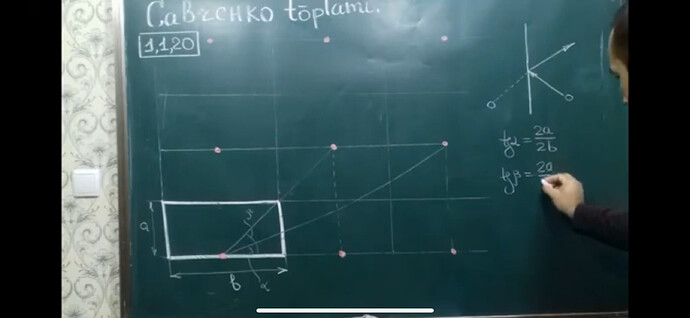
Угол \phi между скоростью и длинной стороной стола
Для У:
V\sin{\phi} \cdot T =2 a \cdot n
По оси У шар должен пройти вниз и вверх, тоесть чётное количество дистанций а.
Для Х:
V \cos{\phi} \cdot T =b \cdot z
Где n и z это целые числа
Оба условия выполняются в один и тот же момент, и можно исключить время из этих уравнений, находя условие для тангенса угла.
6 лайков