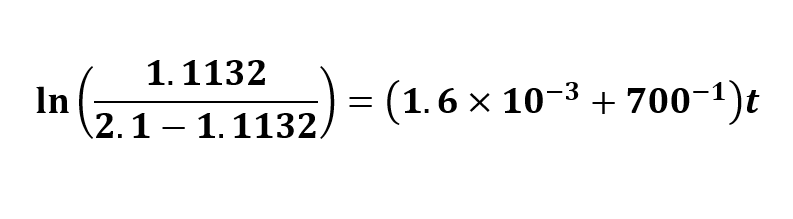Здравствуйте! Помогите, пожалуйста, решить задачу
1 лайк
K=\frac{k_1}{k_{-1}}\\
1.12=\frac{1.6\cdot 10^{-3}}{k_{-1}}\\
k_{-1}=\frac{1.6\cdot 10^{-3}}{1.12}=1.42857\cdot 10^{-3}
Для того чтобы решить эту задачу надо уметь решать интеграл:
\frac{d[A]}{dt}=-k_1[A]+k_{-1}[B]=-k_1+k_{-1}([A]_0-[A])
Из этого выходит:
[A]=\frac{(k_{-1}+k_1\cdot e^{-(k_1+k_1{-1})t})[A]_0}{k_1+k_{-1}}
Можешь взять соотношение \frac{[A]}{[A]_0}=0.7
7 лайков
Если подставить под твое выражение, то получится t=277 с. Твоя ошибка в том, что ты принял, что в начале не было B.
[B]_{0}≠0
[A]_{0}≠[A]+[B] \Rightarrow [B]≠[A]_{0}-[B]
По условию, в начальный момент времени B в три раза меньше чем A
15 лайков
Задачу можно еще решить прикольным путем, который практически не требует всяких трюков с интегрированием. Для этого обозначим x как отклонение от равновесного состояния :
x=\ce{[A] - [A]_{\infin} = [B]_{\infin} - [B]}
Мы знаем, что в равновесии \ce{K = \frac{k_{1}}{k_{-1}} = \frac{[B]_{\infin}}{[A]_{\infin}}}. Другими словами, \ce{[B]_{\infin} = \frac{k_{1}}{k_{-1}}[A]_{\infin}}.
Теперь, напишем кинетическое уравнение для скорости образования вещества \ce{A} :
\ce{\frac{d[A]}{dt} = k_{-1}[B] - k_{1}[A]}
Выразим текущие концентрации веществ \ce{A,B} через отклонение и равновесные концентрации, и получим
\ce{\frac{d[A]}{dt} = k_{-1}([B]_{\infin}-x) - k_{1}([A]_{\infin} + x)}
\ce{\frac{d[A]}{dt} = k_{1}[A]_{\infin} - k_{-1}x -k_{1}[A]_{\infin} - k1x}
\ce{\frac{d[A]}{dt} = -(k_{1} + k_{-1})x}
Обратим внимание на то, что производная x от \ce{[A]} будет равна одному, поэтому \ce{dx = d[A]}, что дает нам
\ce{\frac{dx}{dt} = -(k_{1} + k_{-1})x}
А вот тут даже незнакомому с интегралами олимпиаднику понятно, что интегрированием можно получить :
\ce{ln(\frac{x_{0}}{x})= (k_{1} + k_{-1})t}
Здесь \ce{x_{0}} представляет собой отклонение начальной концентрации от равновесной, и отсюда ты с легкостью можешь выразить текущую концентрацию в-ва \ce{A} или \ce{B}, и продолжить решение.
17 лайков
Спасибо всем 
2 лайка
можно ли найти [A]_{\infty} по этой формуле
[A]_{\infty}= \frac{k_{-1}}{k_1 + k_{-1}} \cdot [A]_0
у меня выходит 277с.
нашел [A]_{\infty} по этой формуле [A]_{\infty}= \frac{k_{-1}}{k_1 + k_{-1}} \cdot [A]_0 вышло 1,416x.
Тогда
ln(\frac{3x-1.416x}{2.1x-1.416x})=(1.6 \cdot10^{-3} +1.43 \cdot10^{-3})t
t=277с
где моя ошибка?
1 лайк
О нет, мы сделали ту же ошибку, которую сделал @DiasTaraz в самом начале… Мы взяли, что \pu{[B]_{0}= 0}! А по условию, \pu{3 [B]_{0}=[A]_{0}}
2 лайка
тогда как решить задачу?
А чем решение @Madsoul тебе не угодило?
мне кажется или похожий вопрос уже задавали
вроде я решил как @Madsoul
1 лайк
Для обратимой реакции A ⇄ B константа равновесия K = 1,12, константа скорости k_1 = 1,6 · 10^{−3}
c^{−1}, в начальный момент времени изомера A в 3 раза больше, чем B. Через какое время концентрация A уменьшится на 30%?
О т в е т. 546 с.
4 лайка
У меня выходит, что равновесная концентрация [A] =1.8868M, тогда подставим в Вашу формулу:
Тогда, выходит, t=39.8 s.
Подскажите, пожалуйста, где ошибка
3 лайка
аа вы в знаменателе отняли отклонение начальной концентрации от равновесной концентрации, вместо равновесной концентрации вещества А.
3 лайка
У меня равновесная вышла [A] =1.8868M, а 2.1М - это 70% от начальной концентрации в-ва А
1 лайк
а почему мы из B равновесного вычитаем В чтобы получить x, а в случае с A наоборот?
1 лайк
Представьте что у вас есть 100 долларов, пока что вы их никуда не потратили, но для достижения равновесия вас побили и отобрали 30, осталось 70, 70 это и есть равновесная концентрация, x=30, 100-70=30, это для А
Случай для В: у вас было 0 долларов но вы побили кого то и взяли 30, для равновесия, 30 это и есть равновесная концентрация а 0 это начальная концентрация В ( денег же не было)
в итоге 30-0=30
То есть, А это когда вас избили, В это когда вы кого то избили, поэтому и наоборот.
6 лайков
коммунизм на минималках
2 лайка