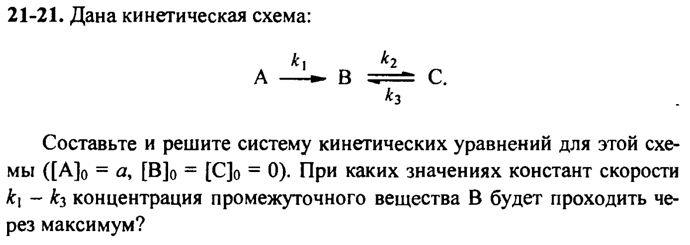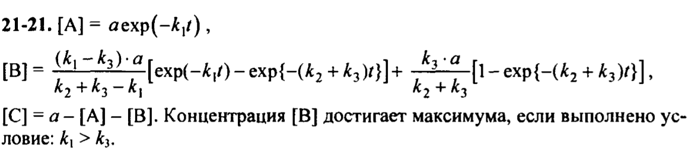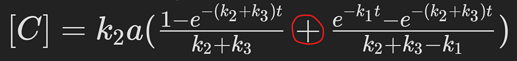При решении задачи я решил вывести зависимость [С] от t, а потом, подставив под выражение [B] = a -[A] - [С], найти зависимость [B] от t. Для [C] вышло вот так:
[C] = k_2a( \frac{1 - e^{-(k_2+k_3)t} }{k_2+k_3} + \frac{e^{-k_1t} -e^{-(k_2+k_3)t} }{k_2+k_3-k_1} )
Несколько раз убедился, что мой ответ правильный, подставляя числа вместо k_1, k_2,k_3,t и a. Но как бы я не старался не смог вывести выражение для [B] хотя значение при подставлении одинаковые. Помогите получить ответ как в книге.
1 лайк
Сходу можно сказать, что выражение для [\text{A}](t) будет такое же, как и в простой реакции распада по первому порядку, потому что \text{A} больше нигде не образуется и нигде не тратится. Поскольку [\text{B}]_0 = [\text{C}]_0 = 0 и в реакции коэффициенты перед всеми тремя соединениями одинаковые, можно выразить [\text{C}] = [\text{A}]_0 - [\text{A}] - [\text{B}]. Для соединения \text{B} можно записать такое дифференциальное уравнение:
\frac{\text{d[B]}}{\text{d}t} = k_1[\text{A}] + k_3[\text{C}] - k_2[\text{B}]
Используя факты, которые я только что перечислил, можно это выражение преобразовать и получить линейное дифференциальное уравнение первого порядка для [\text{B}](t).
Напиши если будут проблемы с решением уравнения или преобразования выражения.
2 лайка
Не хочу казаться токсичным, но как думаешь как бы я решил уравнение для [C] без линейного ДУ? Конечно же я пробовал использовать это и для [B]. Я не смог переобразовать уравнение [B] в линейную дифференциальное уравнение первого порядка. Поэтому решил использовать этот метод для [C] и у меня вышло, то что я написал выше. Вот моя попытка для [B]:
\frac{d[B]}{dt} = k_1ae^{-k_1t}-k_2[B]+k_3[C]
Линейное уравнение имеет вид: y’+p(x)y=q(x). Максимум, что я смог сделать:
[B]'+k_2[B]=k_1ae^{-k_1t}+k_3[C]
1 лайк
Подставь [\text{C}] = [\text{A}]_0 - [\text{A}] - [\text{B}]
2 лайка
Спасибо. Вышло. Не понимаю почему если выводить через [С] выходит другой ответ?
Извени за нетактичность, а откуда задачка?
Еремин основы физхимии
1 лайк