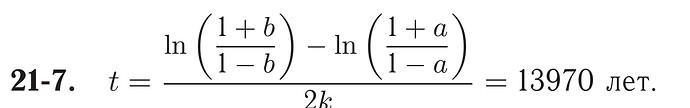Можете показать мою ошибку? Я что-то не учёл?
7 лайков
Твоя ошибка заключается в том, что ты сразу же выразил концентрацию D через концентрацию L, благодаря b. Смысл интегрирования заключается в том, чтобы просуммировать бесконечно малое изменение концентрации L в определенном диапазоне (в данном случае от начальной концентрации L до конечной, для которой и можно написать выражение через b).
Ты начинал решение правильно, записав выражение :
[D]_{0} + [L]_{0}=[D] + [L]
Оно правильное, потому что оно справедливо для любого состава изомеров. Выразим отсюда концентрацию D :
[D] = [D]_{0}+[L]_{0}-[L]
Здесь мы можем выразить начальную концентрацию D через начальную концентрацию L, поскольку они являются константами.
[D]=[L]_{0}(a+1) -[L]
Выражение для скорости образования L выглядит следующим образом :
\frac{d[L]}{dt} = k([D]-[L])
\frac{d[L]}{dt} = k([L]_{0}(a+1) -2[L])
Данный интеграл легко берется заменой функции, поэтому покажу лишь результат :
ln(\frac{[L]_{0}(a+1)-2[L]}{[L]_{0}(a-1)} =-2kt
А вот тут то и можно выразить концентрацию L через b, поскольку интегрировали мы от начальной концентрации до конечной :
[L]_{0}(1+a) = [L](1+b)
[L] = [L]_{0} \frac{(1+a)}{(1+b)}
Отсюда мы и получаем :
ln(\frac{[L]_{0}(a+1)-2[L]_{0} \frac{(1+a)}{(1+b)}}{[L]_{0}(a-1)} =-2kt
ln(\frac{(a+1)-2 \frac{(1+a)}{(1+b)}}{(a-1)}) =-2kt
ln(\frac{(a+1)(1+b)-2(1+a)}{(a-1)(1+b)}) =-2kt
ln(\frac{a+ab+1+b-2-2a}{a+ab-1-b}) = -2kt
ln(\frac{-a+b+ab-1}{a+ab-1-b}) = -2kt
ln(\frac{a+ab-1-b}{-a+ab-1+b}) = 2kt
ln(\frac{1+b}{1-b})-ln(\frac{1+a}{1-a}) = 2kt
Что полностью совпадает с ответом
8 лайков
Спасибо за то что приложил свои попытки решения задачи!
2 лайка
Я чёт не понял объяснения.
Почему нельзя использовать конечное соотношение, а изначальное можно?
1 лайк
Ты не можешь взять и выразить концентрацию в-ва D через концентрацию в-ва L с помощью b в выражении скорости реакции в дифференциальной форме, потому что после смерти организма, a постепенно будет стремиться к b, и поэтому ты не можешь просто так выразить его и проинтегрировать выражение. Если бы ты так сделал, то это бы означало, что в каждый момент времени, концентрация D меньше концентрации L в b раз.
Твоя задача заключается в том, чтобы просуммировать абсолютно все изменения концентрации L от начальной концентрации, до концентрации L, для которой справедливо использовать соотношение с участием b.
Потому что оно постоянное, и не меняется в ходе реакции
5 лайков
@Madsoul уже объяснил, но мне кажется, будет понятнее так: через b выразить [\text{D}] ничего не мешает, но ты вынес b за знак интеграла, подразумевая, что это константа. На деле же, она меняется в процессе реакции, и как раз из-за того, что она меняется в ходе реакции, по ее значению (то есть по соотношению \text{[D]/[L]}) можно сказать, сколько времени прошло с начала реакции.
А вот значение a постоянно, потому что она выражается через начальные концентрации, то есть является соотношением таких же констант.
4 лайка