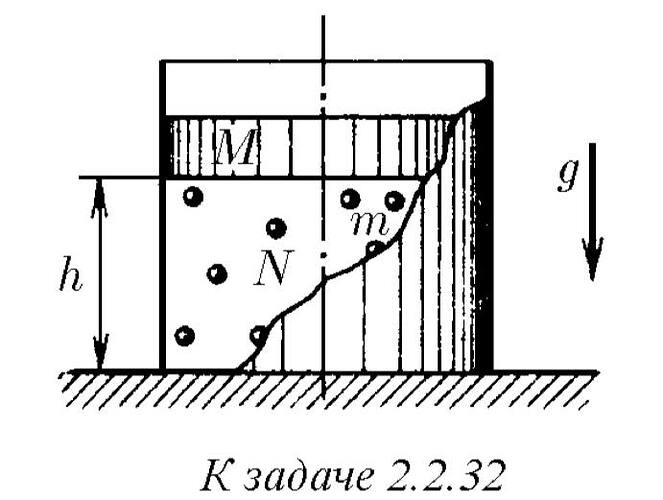
В цилиндре под поршнем массы M прыгают, упруго ударяясь о поршень и дно цилиндра, N шариков массы m каждый. Сила тяжести, действующая на поршень, уравновешена ударами шариков. Расстояние между дном цилиндра и поршнем равно h. Полная энергия каждого шарика одинакова. На какую высоту будут подскакивать шарики, если поршень быстро убрать? N ≫ 1.
Я эту задачу с лета не могу решить тогда я оставил на потом и опять не смог
2 лайка
Задачу можно быстро решить зная минимальную информацию о силе приложенной к поршню от шариков и легкой динамикой.
Для начало проанализируем процесс, когда за промежуток времени когда все N количество шариков успеют ударится о поршень. Интервал между столкновениями первого и последнего шарика о поршень равна тому же количеству времени за которое первый шарик успеет упасть и подняться снова. Следовательно, для начало запишем для начало уравнение изменение импульса за весь процесса:
F=N\frac{\Delta p}{\Delta t}
Помним, что так как каждый шарик имел одинаковую энергию, то у них импульса при столкновении с поршнем будут одинаковы:
p=mv
Так как удар предположительно абсолютно упругий то, с таким и импульсом и будет отталкиваться шарик.
Дальше учитывая первое уравнение время \Delta t за которое шарик успеет отталкнуться и вернуться можно найти время за которое шарик только опускался книз, которое очевидно в два раза меньше \Delta t.
Таким образом, записывается простое уравнение прямолинейного движения шарика с какой - то начальной скорость v вниз.
h=vt+\frac{gt^2}{2}
Не забываем, что сила удара всех шариков равна весу поршня и в конце просто записываем закон сохранения энергии одного шарика до снятий и после снятия поршня.
F=Mg\\
mgH=\frac{mv^2}{2}+mgh
8 лайков
У вас вышло ответ?
Да, вышел.
А почему мы должны рассмотреть в момент когда шарик будет двигаться вниз?
1 лайк
Ну, смотри момент соударение шариков и поршнем когда происходит? На высоте h от дна поршни. И мы знаем, что мы можем поставить произвольную скорость для расчета изменения импульса, учитывая это нам не нужно считать отдельную скорость на дне поршня.
Можешь конечно попробовать найти начальную скорость шарика при уже на дне поршня, но это как по мне это не изменит результат, а только чуть-чуть удлинит ее решение.
Я думал решение будет намного сложнее, @arman_dx аби говорил то что можно взять шариков как молекулы но это сложно(для меня, там используются kT что ли?)
1 лайк
Можно попробовать решить через среднюю энергию частицы, концентрацию частиц, давление(МКТ). Но скорее всего тут нету такой идеи, так как само движение шариков не хаотичное и вроде бы у них всегда меняется кинетическая энергия от дна до поршня при каждом отскоке, но средняя энергия всей системы остается постоянной.
1 лайк
Спасибо большое!
3 лайка